
科目:初中数学 来源:不详 题型:单选题
| A.BD>CD |
| B.BD=CD |
| C.BD<CD |
| D.BD与CD大小关系无法确定 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:解答题

科目:初中数学 来源: 题型:解答题
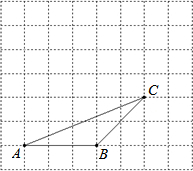 如图,△ABC的三个顶点A、B、C在正方形网格中,每小方格的边长都为
如图,△ABC的三个顶点A、B、C在正方形网格中,每小方格的边长都为科目:初中数学 来源: 题型:
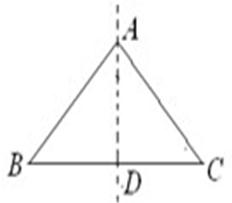 14、做如下操作:在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.
14、做如下操作:在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.①②③ | B.①② | C.①③ | D.②③ |
科目:初中数学 来源:2011年浙江省台州市温岭市温中实验学校中考数学二模试卷(解析版) 题型:填空题

科目:初中数学 来源: 题型:填空题
 做如下操作:在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.
做如下操作:在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com