
科目:初中数学 来源: 题型:
| A、平行 | B、AO垂直且平分BC | C、斜交 | D、AO垂直但不平分BC |
科目:初中数学 来源:不详 题型:单选题
| A.平行 | B.AO垂直且平分BC |
| C.斜交 | D.AO垂直但不平分BC |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
已知:在△ABC中,AB=AC,O为不同于A的一点,且OB=OC,则直线AO与底边BC的关系为( )
A.平行 B.AO垂直且平分BC
C.斜交 D.AO垂直但不平分BC
科目:初中数学 来源: 题型:解答题
 个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
科目:初中数学 来源:2010-2011学年浙教版九年级(上)第三次月考数学试卷(解析版) 题型:解答题
 个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
科目:初中数学 来源:101网校同步练习 初三数学 人教版(新课标2004年初审) 人教实验版 题型:044
如图,在△ABC中,已知AB=BC=CA=4 cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1 cm/s;点Q沿CA、AB向终点B运动,速度为2 cm/s.设它们运动的时间为x(s).

(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系.请写出相应位置关系的x的取值范围(不要求写出过程).
科目:初中数学 来源: 题型:
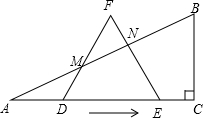 ),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).
),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).科目:初中数学 来源: 题型:解答题
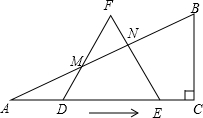 ),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).
),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).科目:初中数学 来源:2012年福建省福州市中考数学模拟试卷(一)(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com