
科目:初中数学 来源:2011-2012学年江苏省无锡市崇安区九年级(上)期中数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:
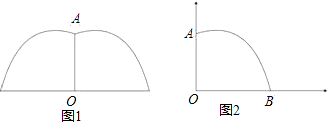
| 4 | 5 |
科目:初中数学 来源: 题型:解答题
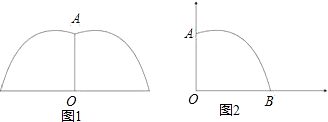
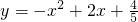 .
.科目:初中数学 来源:2009年湖北省荆州市沙市区中考数学二模试卷(解析版) 题型:解答题
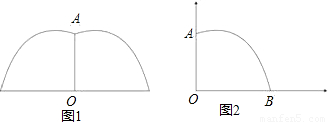
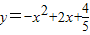 .
.科目:初中数学 来源:江苏省苏州工业园区星海中学2012届九年级中考二模数学试题 题型:044
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
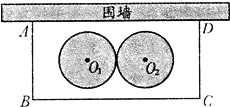
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O1和O2,且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(1)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.
科目:初中数学 来源: 题型:
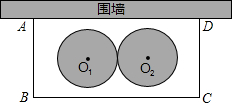 某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.科目:初中数学 来源:四川省中考真题 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com