
科目:初中数学 来源:2013-2014学年北京市门头沟九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,四边形 、
、 是两个边长分别为5和1且中心重合的正方形.其中,正方形
是两个边长分别为5和1且中心重合的正方形.其中,正方形 可以绕中心
可以绕中心 旋转,正方形
旋转,正方形 静止不动.
静止不动.

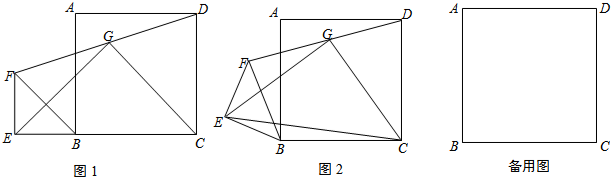
(1)如图1,当 四点共线时,四边形
四点共线时,四边形 的面积为__;
的面积为__;
(2)如图2,当 三点共线时,请直接写出
三点共线时,请直接写出 =
_________;
=
_________;
(3)在正方形 绕中心
绕中心 旋转的过程中,直线
旋转的过程中,直线 与直线
与直线 的位置关系______________,请借助图3证明你的猜想.
的位置关系______________,请借助图3证明你的猜想.
科目:初中数学 来源:不详 题型:解答题
 、
、 是两个边长分别为5和1且中心重合的正方形.其中,正方形
是两个边长分别为5和1且中心重合的正方形.其中,正方形 可以绕中心
可以绕中心 旋转,正方形
旋转,正方形 静止不动.
静止不动.
 四点共线时,四边形
四点共线时,四边形 的面积为__;
的面积为__; 三点共线时,请直接写出
三点共线时,请直接写出 = _________;
= _________; 绕中心
绕中心 旋转的过程中,直线
旋转的过程中,直线 与直线
与直线 的位置关系______________,请借助图3证明你的猜想.
的位置关系______________,请借助图3证明你的猜想.科目:初中数学 来源: 题型:单选题
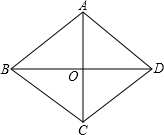 如图,AC,BD是菱形ABCD的对角线,且交于点O,则下面正确的是
如图,AC,BD是菱形ABCD的对角线,且交于点O,则下面正确的是科目:初中数学 来源:同步题 题型:单选题
科目:初中数学 来源: 题型:
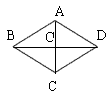
如图,![]() ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,HG∥AB,则下列说法不正确的是( )
ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,HG∥AB,则下列说法不正确的是( )

A.S![]() AEPG=S
AEPG=S![]() PHCF B.图中有3对全等三角形
PHCF B.图中有3对全等三角形
C.图中共有9个平行四边形 D.S![]() AEFD≠S
AEFD≠S![]() GHCD
GHCD
科目:初中数学 来源:同步练习 七年级数学 下册 题型:013
如图,△ABC中,AB=AC,∠BAC=4∠B,AB、AC的中垂线分别交BC于点D、E.给下列四个结论
①△BAE和△CAD是直角三角形
②△ABD和△ACE关于DE的中垂线对称
③△ADE是等边三角形
④△ABD、△ADE、△ACE三个三角形的对称轴共有五条

其中正确的是
[ ]
科目:初中数学 来源: 题型:
| EC |
| GC |
| 2 |
科目:初中数学 来源: 题型:
 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则 ( )
,则 ( )
A.点 一定在射线 一定在射线 上 上 |
B.点 一定在线段 一定在线段 上 上 |
C.点 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
D.点 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
科目:初中数学 来源:2012届北京市海淀区九年级上学期期末考试数学卷 题型:选择题
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则 ( )
,则 ( )

A.点 一定在射线
一定在射线 上
上
B.点 一定在线段
一定在线段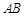 上
上
C.点 可以在射线
可以在射线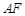 上 ,也可以在线段
上 ,也可以在线段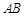 上
上
D.点 可以在射线
可以在射线 上 ,也可以在线段
上 ,也可以在线段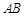 上
上
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com