在平面几何里.有勾股定理:“设△ABC的两边AB.AC互相垂直.则|AB|2+|AC|2=|BC|2 拓展到空间.类比平面几何的勾股定理.“设三棱锥A-BCD的三个侧面ABC.ACD.ADB 两两相互——青夏教育精英家教网—

科目：高中数学 来源： 题型：

3、在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（　　）

A、|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²

B、S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD

C、S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²

D、|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

科目：高中数学 来源：2013-2014学年广东汕头市高二10月月考数学试卷（解析版） 题型：填空题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB²+AC²=BC².”拓展到空间，类比平面几何的勾股定理，研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则 ”．

查看答案和解析>>

科目：高中数学 来源：2013届山东省济宁市高二下学期期中文科数学试卷（解析版） 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB²+AC²=BC²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则可得”猜想正确的是（）

A．AB²+AC²+ AD²=BC² +CD² +BD² B．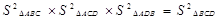

C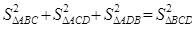． D．AB²×AC²×AD²=BC² ×CD² ×BD²

查看答案和解析>>

科目：高中数学 来源：2010年哈三中高二下学期期末测试数学理 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则”拓展到空间，类比平面几何的勾股定理，“设三棱锥A—BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得” （）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB²+AC²=BC².”拓展到空间，类比平面几何的勾股定理，研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则 ”．

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（　　）

A．|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²

B．S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD

C．S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²

D．|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

查看答案和解析>>

科目：高中数学 来源：2012-2013学年浙江省台州市高二（下）第一次月考数学试卷（文科）（解析版） 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（）
A．|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²
B．S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD
C．S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²
D．|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

查看答案和解析>>

科目：高中数学 来源：2011-2012学年吉林省通化市柳河八中高二（下）模块数学试卷（选修1-2）（解析版） 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（）
A．|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²
B．S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD
C．S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²
D．|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

查看答案和解析>>

科目：高中数学 来源：2009-2010学年黑龙江省哈尔滨三中高二（下）第二学段数学试卷（理科）（解析版） 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（）
A．|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²
B．S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD
C．S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²
D．|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

查看答案和解析>>

科目：高中数学 来源：2012-2013学年山东省淄博市高三复习月考数学试卷5（理科）（解析版） 题型：选择题

在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|²+|AC|²=|BC|²”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（）
A．|AB|²+|AC|²+|AD|²=|BC|²+|CD|²+|BD|²
B．S²_△ABC×S²_△ACD×S²_△ADB=S²_△BCD
C．S_△ABC²+S_△ACD²+S_△ADB²=S_△BCD²
D．|AB|²×|AC|²×|AD|²=|BC|²×|CD|²×|BD|²

查看答案和解析>>

练习册

高中

初中

小学