设数列{an}是首项为b,公比为a(a≠1)的等比数列,Sn是数列{an}的前n项和,对任意的n∈N*,点(Sn,Sn+1)都在直线l上,则直线l的方程是( )| A.y=ax-b | B.y=bx+a | C.y=bx-a | D.y=ax+b |
|
相关习题
科目:高中数学
来源:
题型:
设数列{an}是首项为b,公比为a(a≠1)的等比数列,Sn是数列{an}的前n项和,对任意的n∈N*,点(Sn,Sn+1)都在直线l上,则直线l的方程是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设数列{a
n}是首项为b,公比为a(a≠1)的等比数列,S
n是数列{a
n}的前n项和,对任意的n∈N
*,点(S
n,S
n+1)都在直线l上,则直线l的方程是( )
| A.y=ax-b | B.y=bx+a | C.y=bx-a | D.y=ax+b |
查看答案和解析>>
科目:高中数学
来源:2008年广东省深圳市高级中学高考数学一模试卷(文科)(解析版)
题型:选择题
设数列{an}是首项为b,公比为a(a≠1)的等比数列,Sn是数列{an}的前n项和,对任意的n∈N*,点(Sn,Sn+1)都在直线l上,则直线l的方程是( )
A.y=ax-b
B.y=bx+a
C.y=bx-a
D.y=ax+b
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
设数列{an}是首项为b,公比为a(a≠1)的等比数列,Sn是数列{an}的前n项和,对任意的n∈N*,点(Sn,Sn+1)都在直线l上,则直线l的方程是
- A.
y=ax-b
- B.
y=bx+a
- C.
y=bx-a
- D.
y=ax+b
查看答案和解析>>
科目:高中数学
来源:河南省模拟题
题型:单选题
设数列{an}是首项为1,公比为3的等比数列,把{an}中每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N+,下列结论正确的是
A.b
n+1=3b
n且S
n=
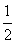
(3
n-1)
B.b
n+1=3b
n-2且S
n=

(3
n-1)
C.b
n+1=3b
n+4且S
n=
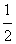
(3
n-1)-2n
D.b
n+1=3b
n-4且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:2010年安徽省高考数学冲刺试卷(文科)(解析版)
题型:选择题
设数列{a
n}是首项为1公比为3的等比数列,把{a
n}中的每一项都减去2后,得到一个新数列{b
n},{b
n}的前n项和为S
n,对任意的n∈N
*,下列结论正确的是( )
A.b
n+1=3b
n,且S
n=

(3
n-1)
B.b
n+1=3b
n-2,且S
n=

(3
n-1)
C.b
n+1=3b
n+4,且S
n=

(3
n-1)-2n
D.b
n+1=3b
n-4,且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:2011年高考数学复习:5.4 数列求和(解析版)
题型:选择题
设数列{a
n}是首项为1公比为3的等比数列,把{a
n}中的每一项都减去2后,得到一个新数列{b
n},{b
n}的前n项和为S
n,对任意的n∈N
*,下列结论正确的是( )
A.b
n+1=3b
n,且S
n=

(3
n-1)
B.b
n+1=3b
n-2,且S
n=

(3
n-1)
C.b
n+1=3b
n+4,且S
n=

(3
n-1)-2n
D.b
n+1=3b
n-4,且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(一)
题型:选择题
设等比数列{an}的首项为a1,公比为q,则“a1<0,且0<q<1”是“对于任意n∈N*都有an+1>an”的(
) ( )
A.充分不必要条件 B.必要不充分条件
C.充分比要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学
来源:宣武区一模
题型:单选题
设等比数列{a
n}的首项为a
1,公比为q,则“a
1<0且0<q<1”是“对于任意n∈N
*都有a
n+1>a
n”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学
来源:宣武区一模
题型:单选题
设等比数列{a
n}的首项为a
1,公比为q,则“a
1<0且0<q<1”是“对于任意n∈N
*都有a
n+1>a
n”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
查看答案和解析>>

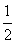 (3n-1)
(3n-1) (3n-1)
(3n-1)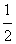 (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n (3n-1)
(3n-1) (3n-1)
(3n-1) (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n (3n-1)
(3n-1) (3n-1)
(3n-1) (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n