练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如表．
    x-3-2-1012345…
    y-24-1006860-10-24…
    则使ax2+bx+c＞0成立的x的取值范围是（　　）
    A．（-10，-1）∪（1+∞）B．（-∞，-1）∪（3+∞）C．（-1，3）D．（0，+∞）
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（x∈R）的最小值为0，且满足条件①f（x-4）=f（2-x），②对任意的x∈R有f（x）≥x，当x∈（0，2）时，f(x)≤(
    x+1
    2
    )2    ，那么f（a）+f（c）-f（b）的值为（　　）
    A、0
    B、
    7
    32
    C、
    9
    16
    D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如表．
    x -3 -2 -1 0 1 2 3 4 5 …
    y -24 -10 0 6 8 6 0 -10 -24 …
    则使ax2+bx+c＞0成立的x的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数 f（x）=ax2+bx+c（x∈R），满足f(0)=f(
    1
    2
    )=0    且f（x）的最小值是-
    1
    8
    ．设数列{an}的前n项和为Sn，对一切（n∈N*），点（n，Sn）在函数f（x）的图象上．
    （1）求数列{an}的通项公式；
    （2）通过bn=
    sn
    n+c
    构造一个新的数列{bn}，是否存在非零常数c，使得{bn}为等差数列；
    （3）令cn=
    sn+n
    n
    ，设数列{cn•2cn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源：2010年江西省南昌市新建二中高考数学二模试卷（文科）（解析版） 题型：选择题

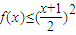    已知二次函数f（x）=ax2+bx+c（x∈R）的最小值为0，且满足条件①f（x-4）=f（2-x），②对任意的x∈R有f（x）≥x，当x∈（0，2）时，，那么f（a）+f（c）-f（b）的值为（ ）
    A．0
    B．
    C．
    D．1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如表．
    x -3 -2 -1 0 1 2 3 4 5 …
    y -24 -10 0 6 8 6 0 -10 -24 …
    则使ax2+bx+c＞0成立的x的取值范围是（　　）
    A．（-10，-1）∪（1+∞）B．（-∞，-1）∪（3+∞）C．（-1，3）D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源：《3.2 函数模型及其应用》2013年同步练习（1）（解析版） 题型：选择题

    已知二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如表．
    x-3-2-112345…
    y-24-10686-10-24…
    则使ax2+bx+c＞0成立的x的取值范围是（ ）
    A．（-10，-1）∪（1+∞）
    B．（-∞，-1）∪（3+∞）
    C．（-1，3）
    D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（a＞0）和一次函数g（x）=kx+m（k≠0），则“f(-
    b
    2a
    )＜g(
    b
    2a
    )    ”是“这两个函数的图象有两个不同交点”的（　　）
    A、必要不充分条件
    B、充分不必要条件
    C、充要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（a＞0）的图象与x轴有两个不同的交点，若f（c）=0，且0＜x＜c时，f（x）＞0
    （1）证明：
    1
    a
    是f（x）的一个根；（2）试比较
    1
    a
    与c的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（a≠0）的导函数为f′（x），且f（-x）=f（x），f（1）=1，f′（-1）=-2．数列{an}满足a1=1，且当n≥2，n∈N*时，an=n2[
    1
    f(1)
    +
    1
    f(2)
    +…+
    1
    f(n-1)
    ]．
    （1）求函数f（x）的解析式；
    （2）当n≥2且n∈N*时，比较
    1+an
    an+1
    与
    f(n+1)
    f(n)
    的大小．
    （3）比较（1+
    1
    a1
    ）（1+
    1
    a2
    ）（1+
    1
    a3
    ）L（1+
    1
    an
    ）与4的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

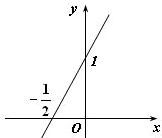    精英家教网已知二次函数f（x）=ax2+bx+c（c＞0）的导函数的图象如图所示：
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）令g(x)=
    f(x)x
    ，求y=g（x）在[1，2]上的最大值．

    查看答案和解析>>


    同步练习册答案