f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且f(-2)=0,则不等式<0的解集为( )| A.(-2,0)∪(2,+∞) | B.(-2,0)∪(0,2) | C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
|
相关习题
科目:高中数学
来源:
题型:
f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且
f(-2)=0,则不等式<0的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且
f(-2)=0,则不等式<0的解集为( )
| A.(-2,0)∪(2,+∞) | B.(-2,0)∪(0,2) | C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
查看答案和解析>>
科目:高中数学
来源:2013-2014学年广西桂林十八中高三(上)第一次月考数学试卷(理科)(解析版)
题型:选择题
f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且

的解集为( )
A.(-2,0)∪(2,+∞)
B.(-2,0)∪(0,2)
C.(-∞,-2)∪(2,+∞)
D.(-∞,-2)∪(0,2)
查看答案和解析>>
科目:高中数学
来源:《导数及其应用》2013年山东省淄博市高三数学复习(理科)(解析版)
题型:选择题
f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且

的解集为( )
A.(-2,0)∪(2,+∞)
B.(-2,0)∪(0,2)
C.(-∞,-2)∪(2,+∞)
D.(-∞,-2)∪(0,2)
查看答案和解析>>
科目:高中数学
来源:
题型:
f(x)和g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)-f(x)g′(x)<0,且f(-2)=0,则不等式
<0的解集为
.
查看答案和解析>>
科目:高中数学
来源:2011年高三数学第一轮基础知识训练(24)(解析版)
题型:解答题
f(x)和g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)-f(x)g′(x)<0,且f(-2)=0,则不等式

的解集为
.
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
f(x)和g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)-f(x)g′(x)<0,且f(-2)=0,则不等式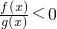 的解集为 ________.
的解集为 ________.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知f(x),g(x),h(x)为一次函数,若对实数x满足
|f(x)|-|g(x)|+h(x)= | | -1,x<-1 | | 3x+2,-1≤x<0 | | -2x+2,x≥0 |
| |
,则h(x)的表达式为( )
| | | |
查看答案和解析>>
科目:高中数学
来源:
题型:
设f(x),g(x)分别是定义在(-∞,0)∪(0,+∞)上的奇函数和偶函数,当x<0时,f(x)•g(x)为单调递增函数,且g(-3)=0,则不等式f(x)•g(x)<0的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知f(x),g(x),h(x)为一次函数,若对实数x满足
|f(x)|-|g(x)|+h(x)= | | -1,x<-1 | | 3x+2,-1≤x<0 | | -2x+2,x≥0 |
| |
,则h(x)的表达式为( )
| A.h(x)=x- | B.h(x)=-x- | C.h(x)=-x+ | D.h(x)=x+ |
查看答案和解析>>

 的解集为( )
的解集为( ) 的解集为( )
的解集为( ) 的解集为 .
的解集为 .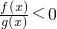 的解集为 ________.
的解集为 ________.