
设(-∞,a)是函数y=x2-4|x|+5的一个减区间,则实数a的取值为( )
|
科目:高中数学 来源: 题型:
| 下列命题: ①设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为-
②关于x的不等式(a-3)x2<(4a-2)x对任意的a∈(0,1)恒成立,则x的取值范围是(-∞,-1]∪[
③变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则r2<0<r1; ④下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
以上命题正确的个数是( ) |
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| 2 |
| 3 |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A.0 | B.1 | C.2 | D.3 |
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:高中数学 来源: 题型:填空题
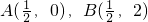 及直线
及直线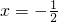 的距离相等,那么满足条件的点P有且只有1个.
的距离相等,那么满足条件的点P有且只有1个.科目:高中数学 来源: 题型:
| x-7 | ||
(a-1)x2+4
|
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 8 |
| π |
| 2 |
| π |
| 3 |
| x |
| 2 |
科目:高中数学 来源:2009-2010学年湖南省长沙市同升湖实验学校高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 ,若x=λx1+(1-λ)x2,记向量
,若x=λx1+(1-λ)x2,记向量 ,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指
,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指 恒成立,其中K是一个正数.
恒成立,其中K是一个正数.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com