练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下列命题：
    ①函数y=2x的图象与函数y=2-x的图象关于y轴对称
    ②函数y=2x的图象与函数y=-2x的图象关于x轴对称
    ③函数y=2x的图象与函数y=-(
    1
    2
    )x    的图象关于原点对称
    ④函数y=2x的图象与函数y=log2x的图象关于直线y=x轴对称
    以上命题中，正确命题的个数为（　　）
    A．1B．2C．3D．4
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：2008-2009学年北京市大兴区高二（下）期末数学试卷（文科）（解析版） 题型：选择题

    下列命题：
    ①函数y=2x的图象与函数y=2-x的图象关于y轴对称
    ②函数y=2x的图象与函数y=-2x的图象关于x轴对称
    ③函数y=2x的图象与函数的图象关于原点对称
    ④函数y=2x的图象与函数y=log2x的图象关于直线y=x轴对称
    以上命题中，正确命题的个数为（ ）
    A．1
    B．2
    C．3
    D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列命题：
    ①函数y=2x与y=log2x互为反函数；
    ②函数y=
    		x2
    与y=log22x是同一个函数；
    ③函数y=2x与y=2-x的图象关于x轴对称；
    ④函数y=
    2x-2-x
    2
    是递增的奇函数．
    其中正确的是
     
    ．（把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：
    ①函数y=
    x-2
    x+2
    的定义域是（-∞，-2]∪[2，+∞）；
    ②若函数y=f（x）在R上递增，则函数y=f（x）的零点至多有一个；
    ③若f（x）是幂函数，且满足
    f(4)
    f(2)
    =3，则f（
    1
    2
    ）=
    1
    3

    ④式子(a-1)-
    1
    2
    有意义，则a的范围是[1，+∞）；
    ⑤任意一条垂直于x轴的直线与函数y=f（x）的图象有且只有一个交点．
    其中正确命题的序号是
    ②③
    ②③
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    有下列命题：
    ①函数y=2x与y=log2x互为反函数；
    ②函数y=
    		x2
    与y=log22x是同一个函数；
    ③函数y=2x与y=2-x的图象关于x轴对称；
    ④函数y=
    2x-2-x
    2
    是递增的奇函数．
    其中正确的是______．（把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省舟山市岱山县大衢中学高一（上）期末数学试卷（解析版） 题型：填空题

    有下列命题：
    ①函数y=2x与y=log2x互为反函数；
    ②函数与y=log22x是同一个函数；
    ③函数y=2x与y=2-x的图象关于x轴对称；
    ④函数是递增的奇函数．
    其中正确的是    ．（把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年浙江省宁波市高一（上）期末数学试卷（解析版） 题型：填空题

    有下列命题：
    ①函数y=2x与y=log2x互为反函数；
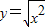    ②函数与y=log22x是同一个函数；
    ③函数y=2x与y=2-x的图象关于x轴对称；
    ④函数是递增的奇函数．
    其中正确的是    ．（把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    有下列命题：①函数y=2x与y=log2x互为反函数；
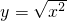    ②函数数学公式与y=log22x是同一个函数；
    ③函数y=2x与y=2-x的图象关于x轴对称；
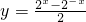    ④函数数学公式是递增的奇函数．
    其中正确的是________．（把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关 Word版训练3-x3练习卷（解析版） 题型：填空题

    给出下列命题：

    ①函数y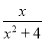＝在区间[1,3]上是增函数；②函数f(x)＝2x－x2的零点有3个；③函数y＝sin x(x∈[－π，π])图象与x轴围成的图形的面积是S＝sin xdx；

    ④若X～N(1，σ2)，且P(0≤X≤1)＝0.3，则P(X≥2)＝0.2，

    其中真命题的序号是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013年山东省烟台市高考数学一模试卷（理科）（解析版） 题型：填空题

    给出下列命题：
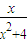    ①函数y=在区间[1，3]上是增函数；
    ②函数f（x）=2x-x2的零点有3个；
    ③函数y=sin x（x∈[-π，π]）图象与x轴围成的图形的面积是S=；
    ④若ξ～N（1，σ2），且P（0≤ξ≤1）=0.3，则P（ξ≥2）=0.2．
    其中真命题的序号是（请将所有正确命题的序号都填上）：    ．

    查看答案和解析>>

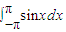    科目：高中数学 来源：2010-2011学年福建省厦门六中高一（上）期中数学试卷（解析版） 题型：填空题

    下列命题：
    ①偶函数的图象一定与y轴相交；
    ②定义在R上的奇函数f（x）必满足f（0）=0；
    ③f（x）=（2x+1）2-2（2x-1）既不是奇函数又不是偶函数；
    ④，则f为A到B的映射；
    ⑤在（-∞，0）∪（0，+∞）上是减函数．
    其中真命题的序号是     （把你认为正确的命题的序号都填上）

    查看答案和解析>>


    同步练习册答案