等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为( ) |
相关习题
科目:高中数学
来源:
题型:
6、等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江西省高三上学期期中考试文科数学试卷(解析版)
题型:选择题
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切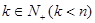 ,都有
,都有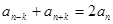 ;
;
③若d>0,则{Sn}中一定有最小的项;
④存在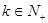 ,使
,使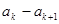 和
和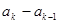 同号。
同号。
其中正确命题的个数为
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列{a
n}的公差d不为0,S
n是其前n项和,给出下列命题:
①若d<0,且S
3=S
8,则S
5和S
6都是{S
n}中的最大项;
②给定n,对于一切k∈N
*(k<n),都有a
n-k+a
n+k=2a
n;
③若d>0,则{S
n}中一定有最小的项;
④存在k∈N
*,使a
k-a
k+1和a
k-a
k-1同号.
其中正确命题的个数为( )
查看答案和解析>>
科目:高中数学
来源:2013年高考数学仿真模拟试卷12(解析版)
题型:选择题
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江西省吉安一中高三(上)期中数学试卷(文科)(解析版)
题型:选择题
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:《2.3 等差数列的前n项和》2011年同步练习(解析版)
题型:选择题
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切k∈N*(k<n),都有an-k+an+k=2an;
③若d>0,则{Sn}中一定有最小的项;
④存在k∈N*,使ak-ak+1和ak-ak-1同号.
其中正确命题的个数为
- A.
4
- B.
3
- C.
2
- D.
1
查看答案和解析>>
科目:高中数学
来源:2004-2005学年北京市东城区高三(上)期末数学试卷(解析版)
题型:解答题
已知等差数列{a
n}的首项a
1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{b
n}的第二项、第三项、第四项.
(I)求数列{a
n}与{b
n}的通项公式;
(Ⅱ)设数列{c
n}对任意正整数n均有

+

+

+…+

=(n+1)a
n+1成立,其中m为不等于零的常数,求数列{c
n}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年黑龙江省虎林高中、密山一中高三第三次联考数学试卷(文科)(解析版)
题型:解答题
已知等差数列{a
n}的首项a
1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{b
n}的第二项、第三项、第四项.
(I)求数列{a
n}与{b
n}的通项公式;
(Ⅱ)设数列{c
n}对任意正整数n均有

+

+

+…+

=(n+1)a
n+1成立,其中m为不等于零的常数,求数列{c
n}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:2006年高考第一轮复习数学:3.4 等差数列与等比数列的综合问题(解析版)
题型:解答题
已知等差数列{a
n}的首项a
1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{b
n}的第二项、第三项、第四项.
(I)求数列{a
n}与{b
n}的通项公式;
(Ⅱ)设数列{c
n}对任意正整数n均有

+
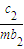
+
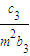
+…+

=(n+1)a
n+1成立,其中m为不等于零的常数,求数列{c
n}的前n项和S
n.
查看答案和解析>>

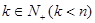 ,都有
,都有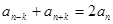 ;
;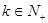 ,使
,使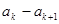 和
和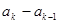 同号。
同号。 +
+ +
+ +…+
+…+ =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn. +
+ +
+ +…+
+…+ =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn. +
+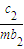 +
+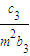 +…+
+…+ =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.