在等差数列{an}中,a1=4,且a1,a5,a13成等比数列,则{an}的通项公式为( )| A.an=3n+1 | B.an=n+3 | | C.an=3n+1或an=4 | D.an=n+3或an=4 |
|
相关习题
科目:高中数学
来源:
题型:
在等差数列{an}中,a1=4,且a1,a5,a13成等比数列,则{an}的通项公式为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在等差数列{a
n}中,a
1=4,且a
1,a
5,a
13成等比数列,则{a
n}的通项公式为( )
| A.an=3n+1 | B.an=n+3 |
| C.an=3n+1或an=4 | D.an=n+3或an=4 |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省东莞七中高二(下)5月月考数学试卷(文科)(解析版)
题型:选择题
在等差数列{an}中,a1=4,且a1,a5,a13成等比数列,则{an}的通项公式为( )
A.an=3n+1
B.an=n+3
C.an=3n+1或an=4
D.an=n+3或an=4
查看答案和解析>>
科目:高中数学
来源:2012-2013学年福建省厦门二中高二(上)数学周末练习4(文科)(解析版)
题型:选择题
在等差数列{an}中,a1=4,且a1,a5,a13成等比数列,则{an}的通项公式为( )
A.an=3n+1
B.an=n+3
C.an=3n+1或an=4
D.an=n+3或an=4
查看答案和解析>>
科目:高中数学
来源:
题型:
在公差非零的等差数列{a
n}中,a
1=4,且a
1,a
5,a
7成等比数列,则该数列{a
n}的通项公式为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在公差非零的等差数列{an}中,a1=4,且a1,a5,a7成等比数列,则该数列{an}的通项公式为______.
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
在公差非零的等差数列{an}中,a1=4,且a1,a5,a7成等比数列,则该数列{an}的通项公式为________.
查看答案和解析>>
科目:高中数学
来源:安徽省江南十校2012届高三最后2套热身试题(一)数学文科试题
题型:013
已知{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=b1=1,a4=7,a5=b2,且存在常数α,β使得对每一个正数n都有an=log,bn+β,则α+β=
[ ]
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
 设集合W由满足下列两个条件的数列{an}构成:
设集合W由满足下列两个条件的数列{an}构成:
①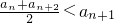 ;②存在实数M,使an≤M.( n为正整数)
;②存在实数M,使an≤M.( n为正整数)
(Ⅰ)在只有5项的有限数列{an}、{bn}中,其中a1=1,a2=2,a3=3,a4=4,a5=5;b1=1,b2=4,b3=5,b4=4,b5=1,试判断数列{an}、{bn}是否为集合W中的元素;
(Ⅱ)设{cn}是等差数列,Sn是其前n项和,c3=4,S3=18,证明数列{Sn}∈W;并写出M的取值范围;
(Ⅲ)设数列{dn}∈W,且对满足条件的常数M,存在正整数k,使dk=M.
求证:dk+1>dk+2>dk+3.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年北京五中高三(上)第二次月考数学试卷(文科)(解析版)
题型:解答题
设集合W由满足下列两个条件的数列{a
n}构成:
①

;②存在实数M,使a
n≤M.( n为正整数)
(Ⅰ)在只有5项的有限数列{a
n}、{b
n}中,其中a
1=1,a
2=2,a
3=3,a
4=4,a
5=5;b
1=1,b
2=4,b
3=5,b
4=4,b
5=1,试判断数列{a
n}、{b
n}是否为集合W中的元素;
(Ⅱ)设{c
n}是等差数列,S
n是其前n项和,c
3=4,S
3=18,证明数列{S
n}∈W;并写出M的取值范围;
(Ⅲ)设数列{d
n}∈W,且对满足条件的常数M,存在正整数k,使d
k=M.
求证:d
k+1>d
k+2>d
k+3.
查看答案和解析>>

 设集合W由满足下列两个条件的数列{an}构成:
设集合W由满足下列两个条件的数列{an}构成: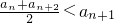 ;②存在实数M,使an≤M.( n为正整数)
;②存在实数M,使an≤M.( n为正整数) ;②存在实数M,使an≤M.( n为正整数)
;②存在实数M,使an≤M.( n为正整数)