设关于x的方程lnx+2x-6=0的实数解为x0,则x0所在的区间是( )| A.(,3) | B.(3,4) | C.(2,) | D.(,2) |
|
相关习题
科目:高中数学
来源:
题型:
设关于x的方程lnx+2x-6=0的实数解为x0,则x0所在的区间是( )
| | | |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设关于x的方程lnx+2x-6=0的实数解为x
0,则x
0所在的区间是( )
| A.(,3) | B.(3,4) | C.(2,) | D.(,2) |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年四川省内江市高一(上)期末数学试卷(解析版)
题型:选择题
设关于x的方程lnx+2x-6=0的实数解为x
,则x
所在的区间是( )
A.
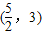
B.(3,4)
C.
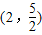
D.
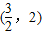
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
设关于x的方程lnx+2x-6=0的实数解为x0,则x0所在的区间是
- A.
- B.
(3,4)
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:四川省南山中学2011-2012学年高一上学期12月月考数学试题(1)
题型:013
设关于x的方程lnx+2x-6=0的实数解为x0,则x0所在的区间是
[ ]
A.
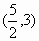
C.
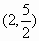
D.
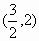
查看答案和解析>>
科目:高中数学
来源:四川省南山中学2011-2012学年高一上学期12月月考数学试题(2)
题型:013
设关于x的方程lnx+2x-6=0的实数解为x0,则x0所在的区间是
[ ]
A.
(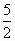 ,3)
,3)
C.
(2,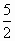 )
)
D.
( ,2)
,2)
查看答案和解析>>
科目:高中数学
来源:云南省建水一中2012届高三11月月考数学理科试题
题型:044
已知函数f(x)=ax·lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省广州市真光中学等六校协作体高三第二次联考数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省广州市真光中学等六校协作体高三第二次联考数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>

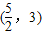
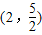
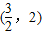
![]()
![]()
![]()
![]() ,3)
,3)![]() )
)![]() ,2)
,2)