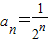练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若{an}为递减数列，则{an}的通项公式可以为（　　）
    A．an=2n+3B．an=-n2+3n+1
    C．an=
    1
    2n
    		D．an=（-1）n
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    若{an}为递减数列，则{an}的通项公式可以为（　　）
    A、an=2n+3
    B、an=-n2+3n+1
    C、an=
    1
    2n
    D、an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若{an}为递减数列，则{an}的通项公式可以为（　　）
    A．an=2n+3B．an=-n2+3n+1
    C．an=
    1
    2n
    		D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省泉州市安溪八中高二（上）期中数学试卷（文科）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建师大附中高二（上）期中数学试卷（文科）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
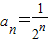
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省泉州市安溪八中高二（上）期中数学试卷（文科）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建师大附中高二（上）期中数学试卷（理科）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省荆州中学高一（下）期中数学试卷（文科）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年北京市东城区高一模块测试数学试卷A（必修5）（解析版） 题型：选择题

    若{an}为递减数列，则{an}的通项公式可以为（ ）
    A．an=2n+3
    B．an=-n2+3n+1
    C．
    D．an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若{an}为递减数列，则{an}的通项公式可以为


    1. A.
      an=2n+3
    2. B.
      an=-n2+3n+1
    3. C.
      数学公式
    4. D.
      an=（-1）n

    查看答案和解析>>

    科目：高中数学 来源：0101 期中题 题型：填空题

    若{an}为递减数列，则{an}的通项公式可能为（    ）（填写序号）。
    ①an=-2n+1；②an=-n2+3n+1；③；④

    查看答案和解析>>


    同步练习册答案