
已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为F1F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e1?e2的取值范围是( )
|
科目:高中数学 来源: 题型:
已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为![]() ,且两条曲线在第一象限的交点为P,
,且两条曲线在第一象限的交点为P,![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源:2012-2013学年河南省高三第三轮适应性考试理科数学试卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为 ,
,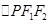 是以
是以 为底边的等腰三角形,若
为底边的等腰三角形,若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,
, ,则
,则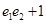 的取值范围是( )
的取值范围是( )
A.(1, ) B.(
) B.( ,
, ) C.(
) C.( ,
, ) D.(
) D.( ,+
,+ )
)
科目:高中数学 来源:2011-2012学年新疆兵团二中高三第五次月考理科数学试卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为 ,且两条曲线在第一象限的交点为P,
,且两条曲线在第一象限的交点为P, 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. 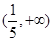 D.
D.

科目:高中数学 来源:2011-2012学年甘肃省高三第一次诊断理科数学试卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为 ,且两条曲线在第一象限的交点为P,
,且两条曲线在第一象限的交点为P,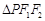 是以
是以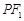 为底边的等腰三角形.若
为底边的等腰三角形.若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是
的取值范围是
A. B.
B. C.
C. 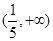 D.
D.
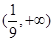
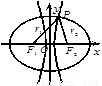
科目:高中数学 来源:2012届河北冀州中学高二年级下学期第三次月考题(理) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为 ,且两条曲线在第一象限的交点为P,
,且两条曲线在第一象限的交点为P, 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为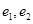 ,则
,则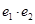 的取值范围是( )
的取值范围是( )
A. B.
B.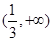 C.
C.
 D.
D.
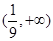
科目:高中数学 来源: 题型:单选题
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为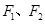 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为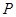 ,
,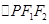 是以
是以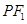 为底边的等腰三角形,若
为底边的等腰三角形,若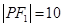 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为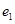 ,
,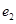 ,则
,则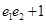 的取值范围是( )
的取值范围是( )
A.(1,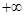 ) ) | B.(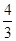 , ,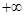 ) ) | C.(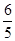 , ,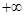 ) ) | D.(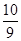 ,+ ,+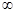 ) ) |
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1,F2,两条曲线在第一象限的交点记为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
A.0,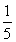 B.
B.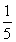 ,
,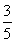 C.
C.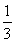 ,+∞ D.
,+∞ D.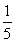 ,+∞
,+∞
科目:高中数学 来源:2010-2011学年河北省衡水市冀州中学高二(下)6月月考数学试卷(理科)(解析版) 题型:选择题
 )
)
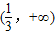
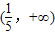
科目:高中数学 来源:2011年福建省福州三中高考数学六模试卷(理科)(解析版) 题型:选择题
 )
)


科目:高中数学 来源:不详 题型:单选题
A.0, | B. , , | C. ,+∞ ,+∞ | D. ,+∞ ,+∞ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com