科目：初中数学 来源： 题型：

2、如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为（　　）

A、32

B、24

C、6

D、8

查看答案和解析>>

科目：初中数学 来源：河南 题型：单选题

如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为（　　）

A．32

B．24

C．6

D．8

查看答案和解析>>

科目：初中数学 来源：2006-2007学年安徽省巢湖市庐江四中九年级（上）期中数学试卷（解析版） 题型：选择题

如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为（）
A．32
B．24
C．6
D．8

查看答案和解析>>

科目：初中数学 来源：2003年河南省中考数学试卷（B卷）（解析版） 题型：选择题

如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为（）
A．32
B．24
C．6
D．8

查看答案和解析>>

科目：初中数学 来源： 题型：单选题

如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为

A.
32
B.
24
C.
6
D.
8

查看答案和解析>>

科目：初中数学 来源：期末题 题型：单选题

[ ]

A.32
B.24
C.6
D.8

查看答案和解析>>

科目：初中数学 来源： 题型：

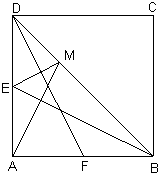如图，正方形ABCD中，E、F分别是AD、AB的中点，过点A作AM⊥BE，交对角线BD于M，连接ME．探究ME与DF之间的位置关系并证明．
说明：
（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．
注意：选取①完成证明得10分；选取②完成证明得5分．
①可画出将△ABE沿BA方向平移BA的长度，再绕点A顺时针旋转90°后的图形；
②∠DEM=∠AEB．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

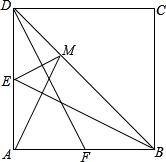如图，正方形ABCD中，E、F分别是AD、AB的中点，过点A作AM⊥BE，交对角线BD于M，连接ME．探究ME与DF之间的位置关系并证明．
说明：
（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．
注意：选取①完成证明得10分；选取②完成证明得5分．
①可画出将△ABE沿BA方向平移BA的长度，再绕点A顺时针旋转90°后的图形；
②∠DEM=∠AEB．

查看答案和解析>>

科目：初中数学 来源：2007年辽宁省大连市甘井子区中考数学模拟试卷（解析版） 题型：解答题

如图，正方形ABCD中，E、F分别是AD、AB的中点，过点A作AM⊥BE，交对角线BD于M，连接ME．探究ME与DF之间的位置关系并证明．
说明：
（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．
注意：选取①完成证明得10分；选取②完成证明得5分．
①可画出将△ABE沿BA方向平移BA的长度，再绕点A顺时针旋转90°后的图形；
②∠DEM=∠AEB．

查看答案和解析>>

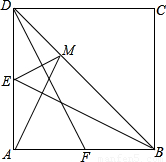
科目：初中数学 来源： 题型：

23、如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．

（如果需要，还可以继续操作、实验与测量）
（1）操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．

（2）观测测量结果，猜测它们之间的关系：

PA=PQ

；
（3）对你猜测的结论是否成立均进行说明理由；
（4）当点P在BC的延长线上移动时，继续（1）的操作实验，试问：（1）中的猜测结论还成立吗？若成立，请给出理由；若不成立，也请说明理由．

查看答案和解析>>

练习册

高中

初中

小学

如果长方形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（-3，2）和（3，2），则该长方形的面积为