练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知A，B，C是平面内的三个点，且AB=3，AC=5，若设BC之间距离为a，则a的取值范围是（　　）
    A．2≤a≤8B．2≤a＜8C．2＜a≤8D．2＜a＜8
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    8、已知A，B，C是平面内的三个点，且AB=3，AC=5，若设BC之间距离为a，则a的取值范围是（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    已知A，B，C是平面内的三个点，且AB=3，AC=5，若设BC之间距离为a，则a的取值范围是（　　）
    A．2≤a≤8B．2≤a＜8C．2＜a≤8D．2＜a＜8

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知A，B，C是平面内的三个点，且AB=3，AC=5，若设BC之间距离为a，则a的取值范围是


    1. A.
      2≤a≤8
    2. B.
      2≤a＜8
    3. C.
      2＜a≤8
    4. D.
      2＜a＜8

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市第一初级中学教育集团2012届九年级中考仿真模拟考试数学试题 题型：044

    如图1，在平面直角坐标系中，已知点A(0，4)，点B在x正半轴上，且∠ABO＝30°．动点P在线段AB上从点A向点B以每秒个单位的速度运动，设运动时间为秒．点M、N在x轴上，且△PMN是等边三角形．

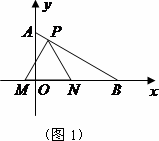
    (1)求点B的坐标；

    (2)求等边△PMN的边长(用的代数式表示)，并求出当等边△PMN的顶点M运动到与原点O重合时的值；

    (3)如果取OB的中点D，以OD为边在Rt△AOB内部作如图2所示的矩形ODCE，点C在线段AB上．设等边△PMN和矩形ODCE重叠部分的面积为S，请求出当0≤t≤2秒时，S与的函数关系式，并求出S的最大值．

    查看答案和解析>>

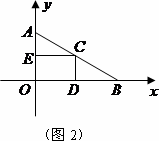
    科目：初中数学 来源： 题型：

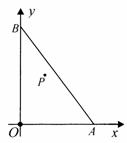
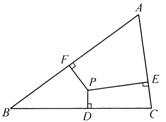
    我们把三角形内部的一个点到这个三角形三边所在直线距离的最小值叫做这个点到这个三角形的距离．如图1，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，如果PE≥PF≥PD，则称PD的长度为点P到△ABC的距离.如图2、图3，在平面直角坐标系中，已知A（6，0），B（0，8），连接AB.

    （1）若P在图2中的坐标为（2，4），则P到OA的距离为      ，P到OB的距离为      ，P到AB的距离为     ，所以P到△AOB的距离为      ；

    （2）若点Q是图2中△AOB的内切圆圆心，求点Q到△AOB距离的最大值；

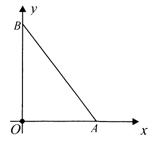    （3）若点R是图3中△AOB内一点，且点R到△AOB的距离为1，请画出所有满足条件的点R所形成的封闭图形，并求出这个封闭图形的周长.（画图工具不限）

    （第23题图1）                （第23题图2）               （第23题图3）
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法正确的个数是（　　）
    ①若AM=
    1
    2
    AB    ，则点M是线段AB的中点；②平角是直线；③平面内，过一点有且只有一条直线与已知直线平行；④平面内，过一点有且只有一条直线与已知直线垂直；⑤两条直线被第三条直线所截，同旁内角互补；⑥点到直线的距离是这点到这条直线的垂线的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

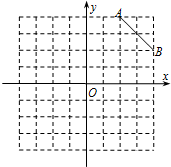    在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．精英家教网点C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
    （1）画出△ABC，点C的坐标是
     
    ，△ABC的面积是
     
    ；
    （2）将△ABC绕点C旋转180°得到△A1B1C，连接AB1、BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6、在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
    （1）填空：C点的坐标是
    （1，1）
    ，△ABC的面积是
    4
    ；
    （2）将△ABC绕点C旋转180°得到△A1B1C1，连接AB1、BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由；
    （3）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2），C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
    （1）填空：C点的坐标是
    （1，1）
    （1，1）
    ，△ABC的面积是
    4
    4
    ；
    （2）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏镇江九年级5月中考模拟数学试卷（带解析） 题型：解答题

    在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．

    【小题1】填空：C点的坐标是　▲　，△ABC的面积是　▲　
    【小题2】将△ABC绕点C旋转180°得到△A1B1C1，连接AB1、BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由；
    【小题3】请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

    查看答案和解析>>


    同步练习册答案