
二次函数的图象通过A(1,0)和B(5,0)两点,但不通过直线y=2x上方的点,则其顶点纵坐标的最大值与最小值的乘积为( )
|
科目:初中数学 来源: 题型:
| A、3 | B、4 | C、5 | D、6 |
科目:初中数学 来源:不详 题型:单选题
| A.3 | B.4 | C.5 | D.6 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
| 5 |
| 2 |
| 3 |
| 2 |
科目:初中数学 来源: 题型:
 已知二次函数已知二次函数y=
已知二次函数已知二次函数y=| 1 | 2 |
科目:初中数学 来源: 题型:解答题
 已知二次函数已知二次函数
已知二次函数已知二次函数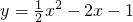
科目:初中数学 来源:2010-2011学年重庆市九龙坡区陶家中学九年级(上)第三次月考数学试卷(解析版) 题型:解答题


科目:初中数学 来源: 题型:
已知如图,二次函数![]()
![]() 图象的顶点为
图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() 、
、![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
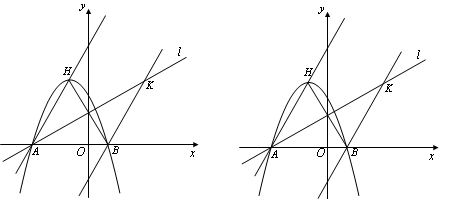
(1)求![]() 、
、![]() 两点坐标,并证明点
两点坐标,并证明点![]() 在直线
在直线![]() 上;
上;
(2)求二次函数解析式;
(3)过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() 、
、![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即![]() 和的最小值
和的最小值
科目:初中数学 来源:2011-2012学年江苏省无锡市新区九年级下学期期中考试数学卷(解析版) 题型:解答题
已知如图,二次函数
 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、 两点(
两点( 在
在 点右侧),点
点右侧),点 、
、 关于直线
关于直线 :
: 对称.
对称.

(1)求 、
、 两点坐标,并证明点
两点坐标,并证明点 在直线
在直线 上;
上;
(2)求二次函数解析式;
(3)过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即 和的最小值
和的最小值
科目:初中数学 来源:2012年初中毕业升学考试(重庆卷)数学(带解析) 题型:解答题
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为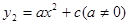 .其图象如图所示.1至6月,污水厂处理每吨污水的费用:
.其图象如图所示.1至6月,污水厂处理每吨污水的费用: (元)与月份x之间满足函数关系式:
(元)与月份x之间满足函数关系式: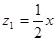 ,该企业自身处理每吨污水的费用:
,该企业自身处理每吨污水的费用: (元)与月份x之间满足函数关系式:
(元)与月份x之间满足函数关系式: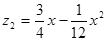 ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出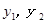 与x之间的函数关系式;
与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a﹣30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.
(参考数据: ≈15.2,
≈15.2,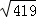 ≈20.5,
≈20.5, ≈28.4)
≈28.4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com