
如果A,B两镇相距8千米,B,C两镇相距10千米,那么C,A两镇相距( )
|
科目:初中数学 来源:不详 题型:单选题
| A.2千米 |
| B.18千米 |
| C.2千米或8千米 |
| D.x千米,2≤x≤18,但x无法确定 |
科目:初中数学 来源:不详 题型:单选题
| A.2千米 |
| B.18千米 |
| C.2千米或8千米 |
| D.x千米,2≤x≤18,但x无法确定 |
科目:初中数学 来源:1995年第7届“五羊杯”初中数学竞赛初三试卷(解析版) 题型:选择题
科目:初中数学 来源:活学巧练 八年级数学 下 题型:044
已知A,B两镇在某县级地图上的距离为13cm,如果它们实际相距26km,试求图上距离与实际距离之比,又如果两村庄之间的图上距离为3cm,求此两村庄之间的实际相距为多少千米?
科目:初中数学 来源: 题型:解答题
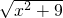 +
+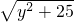 的最小值;
的最小值;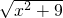 +
+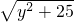 的最小值即为线段______和线段______长度之和的最小值,最小值为______.
的最小值即为线段______和线段______长度之和的最小值,最小值为______.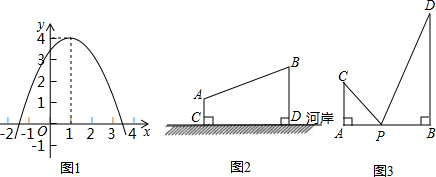
科目:初中数学 来源:2011年河北省石家庄市新华区中考数学一模试卷(解析版) 题型:解答题
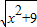 +
+ 的最小值;
的最小值; +
+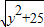 的最小值即为线段______和线段______长度之和的最小值,最小值为______.
的最小值即为线段______和线段______长度之和的最小值,最小值为______.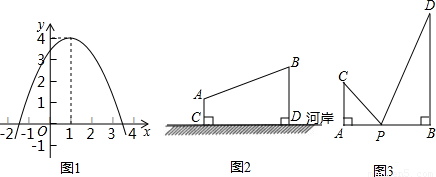
科目:初中数学 来源: 题型:
| x2+9 |
| y2+25 |
| x2+9 |
| y2+25 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com