
若a、b、c、d是乘积为1的4个正数,则代数式a2+b2+c2+d2+ab+ac+ad+bc+bd+cd的最小值为( )
|
科目:初中数学 来源: 题型:
| A、0 | B、4 | C、8 | D、10 |
科目:初中数学 来源:不详 题型:单选题
| A.0 | B.4 | C.8 | D.10 |
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
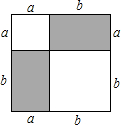 数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题.通过数形结合将代数与几何完美的结合在一起,可以大大降低解题的难度,提高效率和正确率,甚至还可以达到令人意想不到的效果.教科书中利用几何图形证明乘法公式(a+b)2=a2+2ab+b2的做法,就是一个非常典型的例子:
数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题.通过数形结合将代数与几何完美的结合在一起,可以大大降低解题的难度,提高效率和正确率,甚至还可以达到令人意想不到的效果.教科书中利用几何图形证明乘法公式(a+b)2=a2+2ab+b2的做法,就是一个非常典型的例子:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com