
已知⊙O的半径是5,A点为线段PO的中点,当OP=10时,点A与圆的位置关系是( )
|
科目:初中数学 来源:不详 题型:单选题
| A.点A在圆内 | B.点A在圆外 | C.点A在圆上 | D.不能确定 |
科目:初中数学 来源:2007-2008学年山东省烟台市招远市九年级(上)期末数学试卷(解析版) 题型:选择题
科目:初中数学 来源:山东省期末题 题型:单选题
科目:初中数学 来源: 题型:
(14分)已知抛物线y=ax2+bx+c(a≠0)经过A(-2,0)、B(0,1)两点,且对称轴是y轴.经过点C(0,2)的直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.
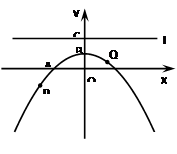
1.(1) 求抛物线的解析式;
2.(2) 以点P为圆心,PO为半径的圆记为⊙P,判断直线l与⊙P的位置关系,并证明你的结论;
3.(3) 设线段PQ=9,G是PQ的中点,求点G到直线l距离的最小值.
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:

科目:初中数学 来源:2011-2012学年福建省福州市九年级上学期期末考试数学卷 题型:解答题
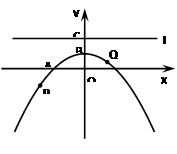
(14分)已知抛物线y=ax2+bx+c(a≠0)经过A(-2,0)、B(0,1)两点,且对称轴是y轴.经过点C(0,2)的直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.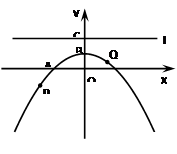
【小题1】(1) 求抛物线的解析式;
【小题2】(2) 以点P为圆心,PO为半径的圆记为⊙P,判断直线l与⊙P的位置关系,并证明你的结论;
【小题3】(3) 设线段PQ=9,G是PQ的中点,求点G到直线l距离的最小值.
科目:初中数学 来源:2011-2012年福建省福州市九年级上学期期末考试数学卷 题型:解答题
(14分)已知抛物线y=ax2+bx+c(a≠0)经过A(-2,0)、B(0,1)两点,且对称轴是y轴.经过点C(0,2)的直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.

1.(1) 求抛物线的解析式;
2.(2) 以点P为圆心,PO为半径的圆记为⊙P,判断直线l与⊙P的位置关系,并证明你的结论;
3.(3) 设线段PQ=9,G是PQ的中点,求点G到直线l距离的最小值.
科目:初中数学 来源: 题型:
 直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.
直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com