
如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过( )
|
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6.
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6.
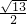 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.科目:初中数学 来源: 题型:解答题
科目:初中数学 来源: 题型:
如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒![]() 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过
点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.

科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(带解析) 题型:解答题
如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒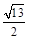 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过
点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,求出此时t的值.
科目:初中数学 来源:2013年浙江省金华市六校联谊中考数学模拟试卷(解析版) 题型:解答题
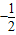 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=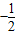 x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点. 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.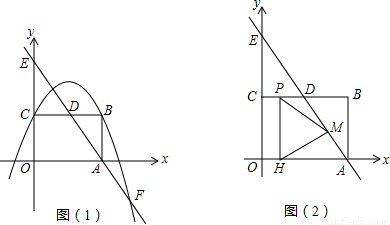
科目:初中数学 来源:2013年江苏省盐城中学中考数学模拟试卷(5月份)(解析版) 题型:解答题
 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6.
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6.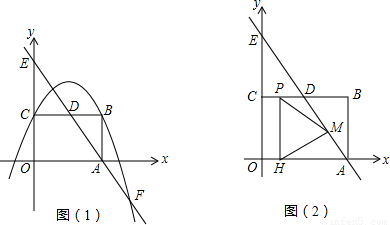
 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.科目:初中数学 来源:2013年湖北省黄冈市中考数学模拟试卷(十五)(解析版) 题型:解答题
 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=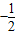 x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点. 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
科目:初中数学 来源:2013年湖北省黄冈市中考数学模拟试卷(八)(解析版) 题型:解答题
 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点. 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
科目:初中数学 来源:2008年北京市延庆县中考数学二模试卷(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com