
已知在同一平面内的四条线段a,b,c,d的长满足
|
科目:初中数学 来源:不详 题型:解答题
|
|

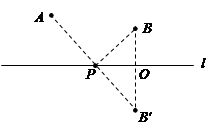 我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
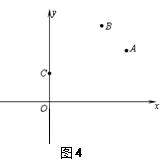

科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 5 |

科目:初中数学 来源:不详 题型:解答题
| 4 |
| 3 |
| 5 |

科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
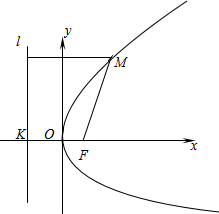 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题. ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.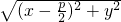 ,d=|x+
,d=|x+ |∴
|∴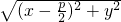 =|x+
=|x+ |
| ,0),它的准线方程是x=-
,0),它的准线方程是x=- .
.| 标准方程 | 交点坐标 | 准线方程 |
| y2=2px(p>0) | (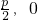 ) ) | x=- |
| y2=-2px(p>0) | (-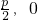 ) ) | x= |
| x2=2py(p>0) | (0, ) ) | y=- |
| x2=-2py(p>0) | (0,- ) ) | y=- |
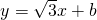 经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.
经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com