
抛物线y=x2+1是由抛物线y=x2+3怎样得到的( )
|
科目:初中数学 来源:同步题 题型:单选题
科目:初中数学 来源: 题型:解答题
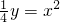 ,即y=4x2(伸缩变换).试回答问题:
,即y=4x2(伸缩变换).试回答问题: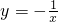 的图象向左平移3个单位,再向下平移4个单位,得到的图象的解析式为______;
的图象向左平移3个单位,再向下平移4个单位,得到的图象的解析式为______; ,得到的图象的解析式为______;
,得到的图象的解析式为______;
科目:初中数学 来源:2009-2010学年浙江省杭州市西湖区丰潭中学九年级(上)期末数学模拟试卷(解析版) 题型:解答题
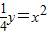 ,即y=4x2(伸缩变换).试回答问题:
,即y=4x2(伸缩变换).试回答问题: 的图象向左平移3个单位,再向下平移4个单位,得到的图象的解析式为______;
的图象向左平移3个单位,再向下平移4个单位,得到的图象的解析式为______; ,得到的图象的解析式为______;
,得到的图象的解析式为______;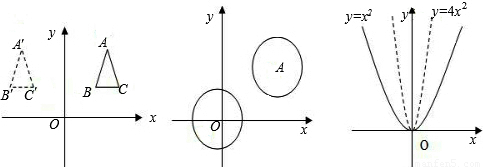
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第1期 总第157期 沪科版 题型:044
将二次函数
y=-科目:初中数学 来源: 题型:解答题
 x2+
x2+ x+
x+ 代成y=a(x-h)2+k的形式;
代成y=a(x-h)2+k的形式; x2+
x2+ x+
x+ 的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的;
的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的; x2+
x2+ x+
x+ 中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)
中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)科目:初中数学 来源:第2章《二次函数》中考题集(18):2.6 何时获得最大利润(解析版) 题型:解答题
 x2+
x2+ x+
x+ 代成y=a(x-h)2+k的形式;
代成y=a(x-h)2+k的形式; x2+
x2+ x+
x+ 的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的;
的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的; x2+
x2+ x+
x+ 中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)
中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)科目:初中数学 来源:第2章《二次函数》中考题集(20):2.3 二次函数的应用(解析版) 题型:解答题
 x2+
x2+ x+
x+ 代成y=a(x-h)2+k的形式;
代成y=a(x-h)2+k的形式; x2+
x2+ x+
x+ 的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的;
的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的; x2+
x2+ x+
x+ 中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)
中,x的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com