
科目:初中数学 来源:2013年江苏省苏州市高级中等学校招生考试数学 题型:044
如图,已知抛物线y=![]() x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
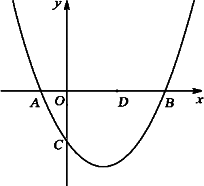
(1)b=________,点B的横坐标为________(上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线y=![]() x2+bx+c交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
x2+bx+c交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有________个.
科目:初中数学 来源:不详 题型:解答题
| x |
| 2 |
| y |
| 3 |
| z |
| 4 |
| 2x+y-z |
| 3x-2y+z |
| 3x2-12 |
| x2+4x+4 |
| a |
| x+2 |
| b |
| x-2 |
| 4x |
| x2-4 |
| 2 |
| x+3 |
| 2 |
| 3-x |
| 2x+18 |
| x2-9 |
科目:初中数学 来源: 题型:
观察可得最简公分母是(x+1)(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【解答】
(2)方程的两边同乘(x+1)(x-1),得
2(x-1)+4=x2-1,
即x2-2x-3=0,
(x-3)(x+1)=0,
解得x1=3,x2=-1,
检验:把x=3代入(x+1)(x-1)=8≠0,即x=3是原分式方程的解,
把x=-1代入(x+1)(x-1)=0,即x=-1不是原分式方程的解,
则原方程的解为:x=3.
【点评】此题考查了![]() 实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
20.(本题满分5分)如图,已知△ABC,且∠ACB=90°。
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明);
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
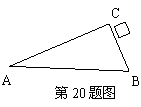 |
科目:初中数学 来源: 题型:
| x |
| 2 |
| y |
| 3 |
| z |
| 4 |
| 2x+y-z |
| 3x-2y+z |
| 3 |
| 4 |
| 3 |
| 4 |
| 3x2-12 |
| x2+4x+4 |
| a |
| x+2 |
| b |
| x-2 |
| 4x |
| x2-4 |
| 2 |
| x+3 |
| 2 |
| 3-x |
| 2x+18 |
| x2-9 |
科目:初中数学 来源: 题型:
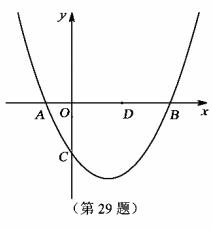
如图,已知抛物线y=![]() x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(1)b= ▲ ,点B的横坐标为 ▲ (上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线y=![]() x2+bx+c交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E
x2+bx+c交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E![]() 三点在同一直线上时,求抛物线的解析式;
三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有 ▲ 个.
科目:初中数学 来源: 题型:解答题
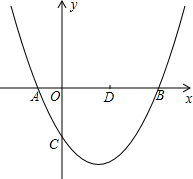 如图,已知抛物线y=
如图,已知抛物线y= x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0). x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;
x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;科目:初中数学 来源:2013年江苏省苏州市中考数学试卷(解析版) 题型:解答题
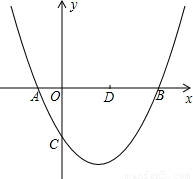 如图,已知抛物线y=
如图,已知抛物线y= x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0). x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;
x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com