
若直线l:y=kx-1与直线x+y-1=0的交点对称的直线方程,则实数k的取值范围是( )
|
科目:高中数学 来源:不详 题型:单选题
| A.(-∞,-1) | B.(-∞,-1] | C.(1,+∞) | D.[1,+∞) |
科目:高中数学 来源:2007-2008学年北京市西城区高三(上)期末数学试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:2010-2011学年广东省广州市东风中学高三数学综合训练试卷8(理科)(解析版) 题型:解答题
科目:高中数学 来源:2007年浙江省杭州市高考数学二模试卷(理科)(解析版) 题型:解答题
科目:高中数学 来源:2009年北京市崇文区高考数学二模试卷(理科)(解析版) 题型:解答题
科目:高中数学 来源:2009年北京市崇文区高考数学二模试卷(文科)(解析版) 题型:解答题
科目:高中数学 来源:教材完全解读 高中数学 必修5(人教B版课标版) 人教B版课标版 题型:044
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
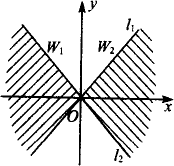
(1)分别用不等式组表示W1和W2;
(2)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(3)设不过原点O的直线l与(2)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点,求证:△OM1M2的重心与△OM3M4的重心重合.
科目:高中数学 来源: 题型:
| y2 |
| a |
| OM |
| ON |
| OQ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com