
在下列条件中,不能说明△ABC≌△A′B′C的是( )
|
科目:初中数学 来源: 题型:
在下列条件中,不能说明△ABC≌△A’B’C’的是( ).
(A)∠A=∠A’,∠C=∠C’,AC=A’C’
(B)∠A=∠A’,AB=A’B’,BC=B’C’
(C)∠B=∠B’,∠C=∠C’,AB=A’B’
(D)AB=A’B’, BC=B’C’,AC=A’C’
科目:初中数学 来源: 题型:
| A.∠A=∠A’,∠C=∠C’,AC=A’C’ |
| B.∠A=∠A’,AB=A’B’,BC=B’C’ |
| C.∠B=∠B’,∠C=∠C’,AB=A’B’ |
| D.AB=A’B’, BC=B’C’,AC=A’C’ |
科目:初中数学 来源:2013届浙江省台州六校八年级第一次联考数学卷(解析版) 题型:选择题
在下列条件中,不能说明△ABC≌△A’B’C’的是( ).
(A)∠A=∠A’,∠C=∠C’,AC=A’C’
(B)∠A=∠A’,AB=A’B’,BC=B’C’
(C)∠B=∠B’,∠C=∠C’,AB=A’B’
(D)AB=A’B’, BC=B’C’,AC=A’C’
科目:初中数学 来源:不详 题型:单选题
| A.∠A=∠A′,∠C=∠C′,AC=A′C′ |
| B.∠A=∠A′,AB=A′B′,BC=B′C′ |
| C.∠B=∠B′,∠C=∠C′,AB=A′B′ |
| D.AB=A′B′,BC=B′C,AC=A′C′ |
科目:初中数学 来源:2011-2012学年浙江省台州六校八年级第一次联考数学卷(带解析) 题型:单选题
在下列条件中,不能说明△ABC≌△A’B’C’的是( ).
| A.∠A=∠A’,∠C=∠C’,AC=A’C’ |
| B.∠A=∠A’,AB=A’B’,BC=B’C’ |
| C.∠B=∠B’,∠C=∠C’,AB=A’B’ |
| D.AB=A’B’, BC=B’C’,AC=A’C’ |
科目:初中数学 来源: 题型:阅读理解

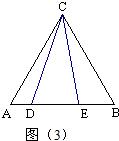
科目:初中数学 来源: 题型:解答题
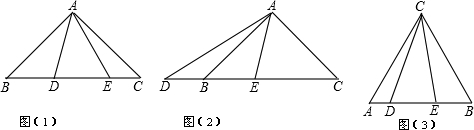
科目:初中数学 来源:2010年中考复习针对性训练 几何探究题(解析版) 题型:解答题
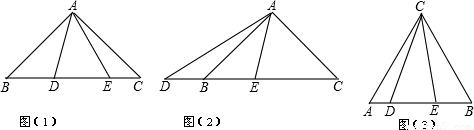
科目:初中数学 来源: 题型:
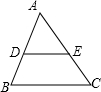 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com