
等差数列(非常数数列)的第2、3、6项顺次成等比数列,则这个等比数列的公比为( )
|
科目:高中数学 来源:2005-2006学年四川省巴中市高一(上)期末数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| 1 |
| an |
| pn+q |
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷4(文科)(解析版) 题型:解答题
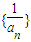 的前n项和为Tn,是否存在正整数p,q,使不等式
的前n项和为Tn,是否存在正整数p,q,使不等式 对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.科目:高中数学 来源:2010年上海市闸北区高三下学期模拟考试(理) 题型:解答题
本题有3小题,第1小题5分,第2小题5分,第3小题9分.
已知定义在 上的函数
上的函数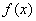 和数列
和数列 满足下列条件:
满足下列条件:
 ,
, ,当
,当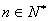 且
且 时,
时, 且
且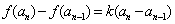 .
.
其中 、
、 均为非零常数.
均为非零常数.
(1)若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)令
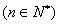 ,若
,若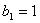 ,求数列
,求数列 的通项公式;
的通项公式;
(3)试研究数列 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
说明:对于第3小题,将根据写出的条件所体现的对问题探究的完整性,给予不同的评分。
科目:高中数学 来源: 题型:
(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分)
已知![]() 是直线
是直线![]() 上的
上的![]() 个不同的点(
个不同的点(![]() ,
,![]() 、
、![]() 均为非零常数),其中数列
均为非零常数),其中数列![]() 为等差数列.
为等差数列.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求证:
,求证: ![]() ;
;
(3) 设![]() ,且当
,且当![]() 时,恒有
时,恒有![]() (
(![]() 和
和![]() 都是不大于
都是不大于![]() 的正整数, 且
的正整数, 且![]() ).试探索:在直线
).试探索:在直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 成立?请说明你的理由.
成立?请说明你的理由.
科目:高中数学 来源: 题型:
(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分.)
平面直角坐标系![]() 中,已知
中,已知![]() ,…,
,…,![]() 是直线
是直线![]() 上的
上的![]() 个点(
个点(![]() ,
,![]() 、
、![]() 均为非零常数).
均为非零常数).
(1)若数列![]() 成等差数列,求证:数列
成等差数列,求证:数列![]() 也成等差数列;
也成等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 满足
满足![]() ,我们称
,我们称![]() 是向量
是向量![]() ,
,![]() ,…,
,…,![]() 的线性组合,
的线性组合,![]() 是该线性组合的系数数列.
是该线性组合的系数数列.
当![]() 是向量
是向量![]() ,
,![]() ,…,
,…,![]() 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:
① 系数数列![]() 需满足怎样的条件,点
需满足怎样的条件,点![]() 会落在直线
会落在直线![]() 上?
上?
② 若点![]() 落在直线
落在直线![]() 上,系数数列
上,系数数列![]() 会满足怎样的结论?
会满足怎样的结论?
③ 能否根据你给出的系数数列![]() 满足的条件,确定在直线
满足的条件,确定在直线![]() 上的点
上的点![]() 的个数或坐标?
的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.【本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分】
科目:高中数学 来源:2010年内蒙古赤峰市高二上学期期中考试数学试卷 题型:选择题
非常数数列 是等差数列,且
是等差数列,且 的第5、10、20项成等比数列,则此等比数列的公比为
( )
的第5、10、20项成等比数列,则此等比数列的公比为
( )
A. B.5 C.2
D.
B.5 C.2
D.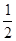
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com