| 已知数列{an}的首项a1=1且满足 n≥2时,an=an-1+,则此数列的第三项是( ) |
相关习题
科目:高中数学
来源:
题型:
已知数列{a
n}的首项a
1=1且满足 n≥2时,a
n=
a
n-1+
,则此数列的第三项是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列{a
n}的首项a
1=1且满足 n≥2时,a
n=
a
n-1+
,则此数列的第三项是( )
查看答案和解析>>
科目:高中数学
来源:2005-2006学年四川省巴中市高一(上)期末数学试卷(解析版)
题型:选择题
已知数列{a
n}的首项a
1=1且满足 n≥2时,a
n=

a
n-1+

,则此数列的第三项是( )
A.1
B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的首项a
1=1,前n项之和S
n满足关系式:3tS
n+1-(2t+3)S
n=3t(t>0,n∈N
*).
(1)求证:数列{a
n}是等比数列;
(2)设数列{a
n}的公比为f(t),数列{b
n}满足
bn+1=f(),(n∈N*),且b
1=1.
(i)求数列{b
n}的通项b
n;
(ii)设T
n=b
1b
2-b
2b
3+b
3b
4-b
4b
5+…+b
2n-1b
2n-b
2nb
2n+1,求T
n.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖北省宜昌市长阳一中高一(下)期中数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n}的首项a
1=1,前n项之和S
n满足关系式:3tS
n+1-(2t+3)S
n=3t(t>0,n∈N
*).
(1)求证:数列{a
n}是等比数列;
(2)设数列{a
n}的公比为f(t),数列{b
n}满足

,且b
1=1.
(i)求数列{b
n}的通项b
n;
(ii)设T
n=b
1b
2-b
2b
3+b
3b
4-b
4b
5+…+b
2n-1b
2n-b
2nb
2n+1,求T
n.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的首项a
1=a,S
n是数列{a
n}的前n项和,且满足:
=3n
2a
n+
,a
n≠0,n≥2,n∈N
*.
(1)若数列{a
n}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{a
n}是递增数列.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的首项a
1=4,且当n≥2时,a
n-1a
n-4a
n-1+4=0,数列{b
n}满足
bn=(n∈N
*)
(Ⅰ)求证:数列{b
n}是等差数列,并求{b
n}的通项公式;
(Ⅱ)若
cn=4bn•(nan-6)(n=1,2,3…),如果对任意n∈N
*,都有
cn+t≤2t2,求实数t的取值范围.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知数列{an}的首项a1=4,且当n≥2时,an-1an-4an-1+4=0,数列{bn}满足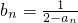 (n∈N*)
(n∈N*)
(Ⅰ)求证:数列{bn}是等差数列,并求{bn}的通项公式;
(Ⅱ)若 (n=1,2,3…),如果对任意n∈N*,都有
(n=1,2,3…),如果对任意n∈N*,都有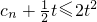 ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列{a
n}的首项a
1=a,S
n是数列{a
n}的前n项和,且满足:
=3n
2a
n+
,a
n≠0,n≥2,n∈N
*.
(1)若数列{a
n}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{a
n}是递增数列.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省淮安市淮阴中学高三(上)期末数学复习试卷(一)(解析版)
题型:解答题
已知数列{a
n}的首项a
1=a,S
n是数列{a
n}的前n项和,且满足:

=3n
2a
n+

,a
n≠0,n≥2,n∈N
*.
(1)若数列{a
n}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{a
n}是递增数列.
查看答案和解析>>

 an-1+
an-1+ ,则此数列的第三项是( )
,则此数列的第三项是( )


 ,且b1=1.
,且b1=1.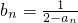 (n∈N*)
(n∈N*) (n=1,2,3…),如果对任意n∈N*,都有
(n=1,2,3…),如果对任意n∈N*,都有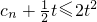 ,求实数t的取值范围.
,求实数t的取值范围. =3n2an+
=3n2an+ ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.