
数轴的定义是( )
|
科目:初中数学 来源: 题型:
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
| ||
| 3 |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
科目:初中数学 来源:2011年福建省厦门市同安区中考数学模拟试卷(一)(解析版) 题型:解答题
 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y= ;
;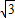 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长; 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.
科目:初中数学 来源:2012年上海市中考数学模拟试卷(一)(解析版) 题型:解答题
 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y= ;
;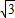 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;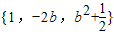 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.
科目:初中数学 来源:2010年浙江省宁波市余姚市中考数学模拟试卷(解析版) 题型:解答题
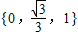 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y= ;
;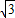 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;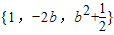 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.
科目:初中数学 来源:2010年四川省绵阳市南山中学实验学校自主招生考试数学试卷(解析版) 题型:解答题
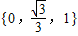 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=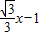 ;
;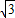 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;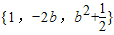 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.
科目:初中数学 来源:2011年3月浙江省杭州市下城区九年级(下)阶段性检测数学试卷(解析版) 题型:解答题
 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y= ;
; 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长; 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.
科目:初中数学 来源: 题型:解答题
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}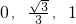 的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y=
的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是y= ;
; 分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长;
分别交于D、C两点,判断以A、B、C、D四点为顶点的四边形形状,请说明理由并计算其周长; 的函数图象的有交点,求满足条件的实数b的取值范围.
的函数图象的有交点,求满足条件的实数b的取值范围.科目:初中数学 来源: 题型:
定义:对于抛物线y=ax2+bx+c ( a、b、c是常数,a≠0),若b2=4ac,则称该抛物线为黄金抛物线.例如:y=2x2-2x+2是黄金抛物线.
(1)请再写出一个与上例不同的黄金抛物线的解析式_ ▲ ;
(2)若抛物线y=ax2+bx+c ( a、b、c是常数,a≠0)是黄金抛物线,请探究该黄金抛物线与x轴的公共点个数的情况(要求说明理由);
(3)将黄金抛物线沿对称轴向下平移3个单位
① 直接写出平移后的新抛物线的解析式;
② 设①中的新抛物线与y轴交于点A,对称轴与x轴交于点B,动点Q在对称轴上,问新抛物线上是否存在点P,使以点P、Q、B为顶点的三角形与△AOB全等?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由
【提示:抛物线y=ax2+bx+c (a≠0)的对称轴是x=-![]() ,顶点坐标是 (-
,顶点坐标是 (-![]() ,
,![]() )】
)】

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com