
△ABC中,AB=AC,且AC上的中线BD把这个三角形的周长分成12和6的两部分,则这个三角形的腰长为( )
|
科目:初中数学 来源:活学巧练七年级数学下 题型:044
如图所示,△ABC中,AB=AC,中线BD把这个三角形的周长分成15cm和11cm两部分,求BC的长.
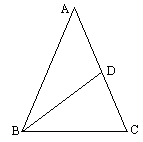
阅读以下解题过程:
解:因为AB=AC,AD=DC=![]() AC=
AC=![]() AB,且
AB,且![]()
所以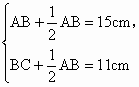
解得 AB=10cm,BC=6cm.
请问:上述解答是否正确?如不正确,请指出错在哪里,应如何改正.
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
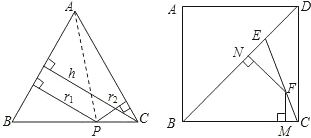
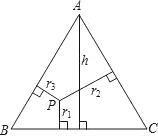
科目:初中数学 来源: 题型:解答题
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).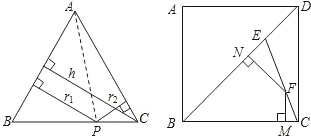

科目:初中数学 来源:2010年河北省唐山市滦南县青坨营中学中考数学模拟试卷(解析版) 题型:解答题
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).
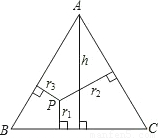
科目:初中数学 来源:2013年四川省内江市全安中学中考数学一模试卷(解析版) 题型:解答题
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).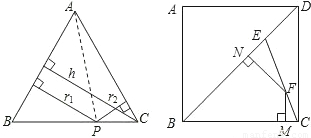
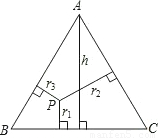
科目:初中数学 来源:2012年山东省德州市平原县中考数学一模试卷(解析版) 题型:解答题
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

科目:初中数学 来源:2012年湖北省咸宁市中考数学模拟试卷(八)(解析版) 题型:解答题
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com