
设a、b、c是三角形的三边,则关于x的一元二次方程cx2+(a+b)x+
|
科目:初中数学 来源: 题型:
若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() 和系数
和系数![]() 有如下关系:
有如下关系:![]() . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
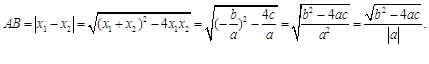
请你参考以上定理和结论,解答下列问题:
设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,显然
,显然![]() 为等腰三角形.
为等腰三角形.
(1)当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求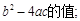
(2)当![]() 为等边三角形时,求
为等边三角形时,求![]()
科目:初中数学 来源: 题型:
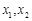 是关于
是关于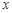 的一元二次方程
的一元二次方程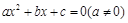 的两个根,则方程的两个根
的两个根,则方程的两个根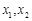 和系数
和系数 有如下关系:
有如下关系: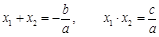 . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数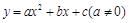 的图象与x轴的两个交点为
的图象与x轴的两个交点为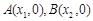 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: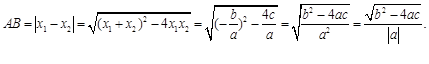
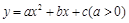 的图象与x轴的两个交点为
的图象与x轴的两个交点为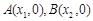 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然 为等腰三角形.
为等腰三角形. 为等腰直角三角形时,求
为等腰直角三角形时,求
 为等边三角形时,求
为等边三角形时,求
科目:初中数学 来源:2012届广东省汕头市濠江区中考模拟考试数学卷(带解析) 题型:解答题
若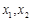 是关于
是关于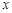 的一元二次方程
的一元二次方程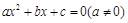 的两个根,则方程的两个根
的两个根,则方程的两个根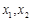 和系数
和系数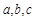 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数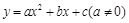 的图象与x轴的两个交点为
的图象与x轴的两个交点为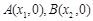 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: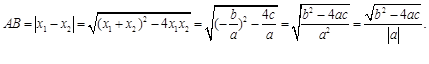
请你参考以上定理和结论,解答下列问题:
设二次函数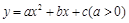 的图象与x轴的两个交点为
的图象与x轴的两个交点为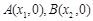 ,抛物线的顶点为
,抛物线的顶点为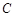 ,显然
,显然 为等腰三角形.
为等腰三角形.
(1)当 为等腰直角三角形时,求
为等腰直角三角形时,求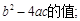
(2)当 为等边三角形时,求
为等边三角形时,求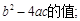
科目:初中数学 来源:2011-2012学年广东省汕头市濠江区中考模拟考试数学卷(解析版) 题型:解答题
若 是关于
是关于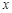 的一元二次方程
的一元二次方程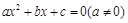 的两个根,则方程的两个根
的两个根,则方程的两个根 和系数
和系数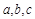 有如下关系:
有如下关系: .
我们把它们称为根与系数关系定理. 如果设二次函数
.
我们把它们称为根与系数关系定理. 如果设二次函数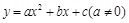 的图象与x轴的两个交点为
的图象与x轴的两个交点为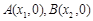 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
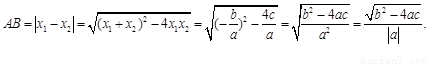
请你参考以上定理和结论,解答下列问题:
设二次函数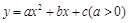 的图象与x轴的两个交点为
的图象与x轴的两个交点为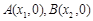 ,抛物线的顶点为
,抛物线的顶点为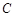 ,显然
,显然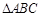 为等腰三角形.
为等腰三角形.
(1)当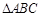 为等腰直角三角形时,求
为等腰直角三角形时,求
(2)当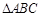 为等边三角形时,求
为等边三角形时,求
科目:初中数学 来源:不详 题型:单选题
| c |
| 4 |
| A.方程有两个相等实根 |
| B.方程有两个不等的正实根 |
| C.方程有两个不等的负实根 |
| D.方程无实根 |
科目:初中数学 来源: 题型:
若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() 和系数
和系数![]() 有如下关系:
有如下关系:![]() . 我们把它们称为根与系数关系定理.
. 我们把它们称为根与系数关系定理.
如果设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:

请你参考以上定理和结论,解答下列问题:
设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,显然
,显然![]() 为等腰三角形.
为等腰三角形.
(1)当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]()
(2)当![]() 为等边三角形时,求
为等边三角形时,求![]()
科目:初中数学 来源:2009-2010学年四川省雅安中学九年级(上)期中数学试卷(解析版) 题型:选择题
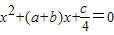 的根的情况是( )
的根的情况是( )科目:初中数学 来源: 题型:单选题
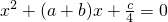 的根的情况是
的根的情况是科目:初中数学 来源:甘肃省中考真题 题型:解答题
 ,x1﹒x2=
,x1﹒x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为: =
=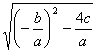 =
=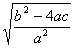 =
= .
. 0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
科目:初中数学 来源:2011-2012学年江苏省九年级课程结束考试数学卷 题型:选择题
如图,正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( ▲ )

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com