
已知关于x的方程x2-(2k-1)x+k2=0有两个不相等的实数根,那么k的最大整数值是( )
|
科目:初中数学 来源: 题型:
| m | x |
科目:初中数学 来源: 题型:
| k |
| 2 |
1-
|
科目:初中数学 来源: 题型:
| 13 |
| 2 |
| 9 |
| 4 |
科目:初中数学 来源: 题型:
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a |
| a |
| a+1 |
| 4 |
| a+1 |
科目:初中数学 来源: 题型:
(10分)已知关于x的方程X2+2KX+K2+2K-2=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若以方程X2+2KX+K2+2K-2=0的两个根为横坐标、纵坐标的点恰在反比例函数![]() 的
的
图象上,求满足条件的m的最小值.
科目:初中数学 来源: 题型:
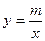 的
的科目:初中数学 来源:2012届初中毕业生第一次月考数学试卷 题型:解答题
(10分)已知关于x的方程X2+2KX+K2+2K-2=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若以方程X2+2KX+K2+2K-2=0的两个根为横坐标、纵坐标的点恰在反比例函数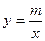 的
的
图象上,求满足条件的m的最小值.
科目:初中数学 来源:2011-2012学年初中毕业生第一次月考数学试卷 题型:解答题
(10分)已知关于x的方程X2+2KX+K2+2K-2=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若以方程X2+2KX+K2+2K-2=0的两个根为横坐标、纵坐标的点恰在反比例函数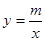 的
的
图象上,求满足条件的m的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com