| 如果方程ax2+bx+c=0(a≠0)的二根是x1、x2,那么x1+x2=-,x1?x2=.若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1?x2的值是( ) |
相关习题
科目:初中数学
来源:
题型:
如果方程ax
2+bx+c=0(a≠0)的二根是x
1、x
2,那么
x1+x2=-,
x1•x2=.若设方程3x
2-6x-7=0的两根是x
1、x
2,由此得x
1+x
2+x
1•x
2的值是( )
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
如果一元二次方程ax2+bx+c=0的两根x1、x2均为正数,且满足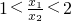 (其中x1>x2),那么称这个方程有“邻近根”.
(其中x1>x2),那么称这个方程有“邻近根”.
(1)判断方程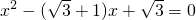 是否有“邻近根”,并说明理由;
是否有“邻近根”,并说明理由;
(2)已知关于x的一元二次方程mx2-(m-1)x-1=0有“邻近根”,求m的取值范围.
查看答案和解析>>
科目:初中数学
来源:不详
题型:单选题
如果方程ax
2+bx+c=0(a≠0)的二根是x
1、x
2,那么
x1+x2=-,
x1•x2=.若设方程3x
2-6x-7=0的两根是x
1、x
2,由此得x
1+x
2+x
1•x
2的值是( )
查看答案和解析>>
科目:初中数学
来源:2010-2011学年四川省遂宁市城区初中九年级(上)期末数学试卷(解析版)
题型:选择题
如果方程ax
2+bx+c=0(a≠0)的二根是x
1、x
2,那么
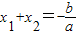
,

.若设方程3x
2-6x-7=0的两根是x
1、x
2,由此得x
1+x
2+x
1•x
2的值是( )
A.

B.

C.-4

D.
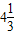
查看答案和解析>>
科目:初中数学
来源:2010-2011学年四川省遂宁市九年级(上)期末数学试卷(解析版)
题型:选择题
如果方程ax
2+bx+c=0(a≠0)的二根是x
1、x
2,那么
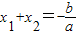
,
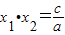
.若设方程3x
2-6x-7=0的两根是x
1、x
2,由此得x
1+x
2+x
1•x
2的值是( )
A.

B.
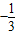
C.-4

D.
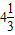
查看答案和解析>>
科目:初中数学
来源:2013年福建省厦门市思明区中考数学一模试卷(解析版)
题型:解答题
如果一元二次方程ax
2+bx+c=0的两根x
1、x
2均为正数,且满足

(其中x
1>x
2),那么称这个方程有“邻近根”.
(1)判断方程

是否有“邻近根”,并说明理由;
(2)已知关于x的一元二次方程mx
2-(m-1)x-1=0有“邻近根”,求m的取值范围.
查看答案和解析>>
科目:初中数学
来源:
题型:阅读理解
阅读材料:在一元二次方程ax
2+bx+c=0(a≠0)中,如果b
2-4ac≥0,记它的两个根为x
1,x
2,由求根公式计算两个根的和与积为x
1+x
2=-
,x
1•x
2=
,一元二次方程两个根的和、两个根的积是由方程的系数确定的,这就是一元二次方程根与系数的关系.根据这段材料解决下列问题:
(1)设方程2x
2-4x-1=0的两个根分别为x
1,x
2,则x
1+x
2=
2
2
,x
1•x
2=
.
(2)如果方程x
2+bx-1=0的一个根是2+
,求方程的另一个根和实数b的值.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
阅读材料:在一元二次方程ax2+bx+c=0(a≠0)中,如果b2-4ac≥0,记它的两个根为x1,x2,由求根公式计算两个根的和与积为x1+x2=- ,x1•x2=
,x1•x2= ,一元二次方程两个根的和、两个根的积是由方程的系数确定的,这就是一元二次方程根与系数的关系.根据这段材料解决下列问题:
,一元二次方程两个根的和、两个根的积是由方程的系数确定的,这就是一元二次方程根与系数的关系.根据这段材料解决下列问题:
(1)设方程2x2-4x-1=0的两个根分别为x1,x2,则x1+x2=______,x1•x2=______.
(2)如果方程x2+bx-1=0的一个根是2+ ,求方程的另一个根和实数b的值.
,求方程的另一个根和实数b的值.
查看答案和解析>>
科目:初中数学
来源:
题型:
如果x
1、x
2是一元二次方程ax
2+bx+c=0的两根,那么有
x1+x2=-,
x1x2=.
这是一元二次方程根与系数的关系,我们利用它可以用来解题.
例:x
1、x
2是方程x
2+4x-6=0的两根,求
+的值.
解:∵x
1+x
2=-4;x
1x
2=-6,则
+=(x1+x2)2-2x1x2=(-4)2-2×(-6)=28.
请你根据以上解法解答下题,已知x
1、x
2是方程2x
2+8x-13=0的两根,求:
(1)
+的值;
(2)
+x1•x2+的值.
查看答案和解析>>

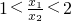 (其中x1>x2),那么称这个方程有“邻近根”.
(其中x1>x2),那么称这个方程有“邻近根”.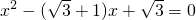 是否有“邻近根”,并说明理由;
是否有“邻近根”,并说明理由;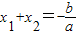 ,
, .若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是( )
.若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是( )


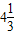
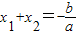 ,
,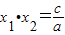 .若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是( )
.若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是( )
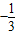

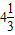
 (其中x1>x2),那么称这个方程有“邻近根”.
(其中x1>x2),那么称这个方程有“邻近根”. 是否有“邻近根”,并说明理由;
是否有“邻近根”,并说明理由;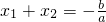 ,
,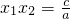 .若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是
.若设方程3x2-6x-7=0的两根是x1、x2,由此得x1+x2+x1•x2的值是
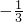

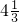
 ,x1•x2=
,x1•x2= ,一元二次方程两个根的和、两个根的积是由方程的系数确定的,这就是一元二次方程根与系数的关系.根据这段材料解决下列问题:
,一元二次方程两个根的和、两个根的积是由方程的系数确定的,这就是一元二次方程根与系数的关系.根据这段材料解决下列问题: ,求方程的另一个根和实数b的值.
,求方程的另一个根和实数b的值.