定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10x+1),x∈(-∞,+∞),那么( )| A.g(x)=x,h(x)=lg(10x+10x+2) | | B.g(x)=[lg(10x+1)+x]h(x)=[lg(10x+1)-x] | | C.g(x)=,h(x)=lg(10x+1)- | | D.g(x)=-,h(x)=lg(10x+1)+ |
|
相关习题
科目:高中数学
来源:
题型:
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10x+1),x∈(-∞,+∞),那么( )
| A、g(x)=x,h(x)=lg(10x+10x+2) |
| B、g(x)=[lg(10x+1)+x]h(x)=[lg(10x+1)-x] |
| C、g(x)=,h(x)=lg(10x+1)- |
| D、g(x)=-,h(x)=lg(10x+1)+ |
查看答案和解析>>
科目:高中数学
来源:
题型:
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)的和,如果f(x)=lg(10x+1),x∈(-∞,+∞),求g(x)与h(x).
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)的和,如果f(x)=lg(10x+1),x∈(-∞,+∞),求g(x)与h(x).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10
x+1),x∈(-∞,+∞),那么( )
| A.g(x)=x,h(x)=lg(10x+10x+2) |
| B.g(x)=[lg(10x+1)+x]h(x)=[lg(10x+1)-x] |
| C.g(x)=,h(x)=lg(10x+1)- |
| D.g(x)=-,h(x)=lg(10x+1)+ |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省安庆市潜山中学高一(上)期中数学试卷(解析版)
题型:选择题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10
x+1),x∈(-∞,+∞),那么( )
A.g(x)=x,h(x)=lg(10
x+10
x+2)
B.g(x)=

[lg(10
x+1)+x]h(x)=

[lg(10
x+1)-x]
C.g(x)=

,h(x)=lg(10
x+1)-

D.g(x)=-

,h(x)=lg(10
x+1)+

查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省安庆市潜山中学高一(上)期中数学试卷(解析版)
题型:选择题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10
x+1),x∈(-∞,+∞),那么( )
A.g(x)=x,h(x)=lg(10
x+10
x+2)
B.g(x)=

[lg(10
x+1)+x]h(x)=

[lg(10
x+1)-x]
C.g(x)=
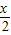
,h(x)=lg(10
x+1)-
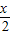
D.g(x)=-
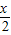
,h(x)=lg(10
x+1)+
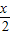
查看答案和解析>>
科目:高中数学
来源:2011年高三数学复习(第2章 函数):2.5 函数的奇偶性(解析版)
题型:解答题
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)的和,如果f(x)=lg(10x+1),x∈(-∞,+∞),求g(x)与h(x).
查看答案和解析>>
科目:高中数学
来源:1994年全国统一高考数学试卷(文科)(解析版)
题型:选择题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10
x+1),x∈(-∞,+∞),那么( )
A.g(x)=x,h(x)=lg(10
x+10
x+2)
B.g(x)=

[lg(10
x+1)+x]h(x)=

[lg(10
x+1)-x]
C.g(x)=
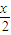
,h(x)=lg(10
x+1)-
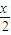
D.g(x)=-

,h(x)=lg(10
x+1)+

查看答案和解析>>
科目:高中数学
来源:1994年全国统一高考数学试卷(理科)(解析版)
题型:选择题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10
x+1),x∈(-∞,+∞),那么( )
A.g(x)=x,h(x)=lg(10
x+10
x+2)
B.g(x)=

[lg(10
x+1)+x]h(x)=

[lg(10
x+1)-x]
C.g(x)=

,h(x)=lg(10
x+1)-

D.g(x)=-
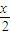
,h(x)=lg(10
x+1)+

查看答案和解析>>
科目:高中数学
来源:
题型:单选题
定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10x+1),x∈(-∞,+∞),那么
- A.
g(x)=x,h(x)=lg(10x+10x+2)
- B.
g(x)=

[lg(10
x+1)+x]h(x)=

[lg(10
x+1)-x]
- C.
g(x)=

,h(x)=lg(10
x+1)-

- D.
g(x)=-

,h(x)=lg(10
x+1)+

查看答案和解析>>

 [lg(10x+1)+x]h(x)=
[lg(10x+1)+x]h(x)= [lg(10x+1)-x]
[lg(10x+1)-x] ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-
 ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+
 [lg(10x+1)+x]h(x)=
[lg(10x+1)+x]h(x)= [lg(10x+1)-x]
[lg(10x+1)-x]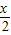 ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-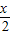
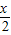 ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+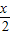
 [lg(10x+1)+x]h(x)=
[lg(10x+1)+x]h(x)= [lg(10x+1)-x]
[lg(10x+1)-x]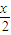 ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-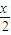
 ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+
 [lg(10x+1)+x]h(x)=
[lg(10x+1)+x]h(x)= [lg(10x+1)-x]
[lg(10x+1)-x] ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-
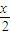 ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+
 [lg(10x+1)+x]h(x)=
[lg(10x+1)+x]h(x)= [lg(10x+1)-x]
[lg(10x+1)-x] ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-
 ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+