练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知三个不等式：ab＞0，bc-ad＞0，
    c
    a
    -
    d
    b
    ＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（　　）
    A．0B．1C．2D．3
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    已知三个不等式：ab＞0，bc-ad＞0，
    c
    a
    -
    d
    b
    ＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源：北京 题型：单选题

    已知三个不等式：ab＞0，bc-ad＞0，
    c
    a
    -
    d
    b
    ＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源：2007年浙江省杭州市高考数学一模试卷（理科）（解析版） 题型：选择题

    已知三个不等式：ab＞0，bc-ad＞0，-＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：2011年高考数学复习：6.1 不等关系与不等式（解析版） 题型：选择题

    已知三个不等式：ab＞0，bc-ad＞0，-＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：2006年高考第一轮复习数学：6.1 不等式的性质（解析版） 题型：选择题

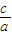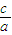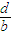    已知三个不等式：ab＞0，bc-ad＞0，-＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：2004年北京市春季高考数学试卷（理科）（解析版） 题型：选择题

    已知三个不等式：ab＞0，bc-ad＞0，-＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三个不等式：①ab＞0;②-＜-;③bc-ad＞0.以其中两个作条件，余下一个作结论，则可组成_____________个正确命题.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三个不等式：ab＞0，bc－ad＞0，－＞0(其中a、b、c、d均为实数)，用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是(　　)

    A．0　　　　                       B．1　　　　

    C．2　　　　                       D．3

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年本溪县高二暑期补课阶段考试数学卷 题型：选择题

    已知三个不等式：ab＞0，bc－ad＞0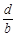，－＞0（其中a、b、c、d均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是

    A.0                 B.1                 C.2                 D.3

     

    查看答案和解析>>

    科目：高中数学 来源：教材完全解读　高中数学　必修5(人教B版课标版) 人教B版课标版 题型：013

    已知三个不等式：ab＞0，bc－ad＞0，－＞0(其中a、b、c、d均为实数)，用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是

    [　　]

    A．0

    B．1

    C．2

    D．3

    查看答案和解析>>


    同步练习册答案