| 求以抛物线y2=8x的焦点为焦点,且离心率为的椭圆的标准方程为( ) |
相关习题
科目:高中数学
来源:
题型:
求以抛物线y
2=8x的焦点为焦点,且离心率为
的椭圆的标准方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
求以抛物线y
2=8x的焦点为焦点,且离心率为
的椭圆的标准方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
求以抛物线y
2=8x的焦点为焦点,且离心率为
的椭圆的标准方程为( )
查看答案和解析>>
科目:高中数学
来源:2007年重庆市南开中学高考数学一模试卷(文科)(解析版)
题型:选择题
求以抛物线y
2=8x的焦点为焦点,且离心率为

的椭圆的标准方程为( )
A.

B.
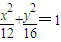
C.
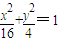
D.
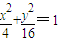
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
求以抛物线y2=8x的焦点为焦点,且离心率为 的椭圆的标准方程为
的椭圆的标准方程为
- A.
- B.
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2013•海口二模)椭圆C以抛物线y2=8x的焦点为右焦点,且经过点A(2,3).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若F1,F2分别为椭圆的左右焦点,求∠F1AF2的角平分线所在直线的方程.
查看答案和解析>>
科目:高中数学
来源:2011年广东省广州市高考数学查漏补缺试卷(理科)(解析版)
题型:解答题
如图,抛物线C
1:y
2=8x与双曲线
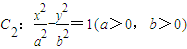
有公共焦点F
2,点A是曲线C
1,C
2在第一象限的交点,且|AF
2|=5.
(1)求双曲线C
2的方程;
(2)以F
1为圆心的圆M与双曲线的一条渐近线相切,圆N:(x-2)
2+y
2=1.已知点
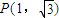
,过点P作互相垂直且分别与圆M、圆N相交的直线l
1和l
2,设l
1被圆M截得的弦长为s,l
2被圆N截得的弦长为t.

是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学
来源:2010年广东省广州市高考数学考前查漏补缺试卷(文科)(解析版)
题型:解答题
如图,抛物线C
1:y
2=8x与双曲线

有公共焦点F
2,点A是曲线C
1,C
2在第一象限的交点,且|AF
2|=5.
(1)求双曲线C
2的方程;
(2)以F
1为圆心的圆M与双曲线的一条渐近线相切,圆N:(x-2)
2+y
2=1.已知点
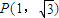
,过点P作互相垂直且分别与圆M、圆N相交的直线l
1和l
2,设l
1被圆M截得的弦长为s,l
2被圆N截得的弦长为t.

是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:

一青蛙从点A
0(x
0,y
0)开始依次水平向右和竖直向上跳动,其落点坐标依次是A
i(x
i,y
i)(i∈N
*),(如图所示,A
0(x
0,y
0)坐标以已知条件为准),S
n表示青蛙从点A
0到点A
n所经过的路程.
(1)若点A
0(x
0,y
0)为抛物线y
2=2px(p>0)准线上一点,点A
1,A
2均在该抛物线上,并且直线A
1A
2经过该抛物线的焦点,证明S
2=3p.
(2)若点A
n(x
n,y
n)要么落在y=x所表示的曲线上,要么落在y=x
2所表示的曲线上,并且
A0(,),试写出
Sn(不需证明);
(3)若点A
n(x
n,y
n)要么落在
y=2-1所表示的曲线上,要么落在
y=2+1所表示的曲线上,并且A
0(0,4),求S
n的表达式.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2013•成都二模)巳知椭圆E:
+=1(a>b>0)(a>b>0)以抛物线y
2=8x的焦点为顶点,且离心率为
(I)求椭圆E的方程
(II)若F为椭圆E的左焦点,O为坐标原点,直线l:y=kx+m与椭圆E相交于A、B 两点,与直线x=-4相交于Q点,P是椭圆E上一点且满足
=+,证明
.为定值并求出该值.
查看答案和解析>>

 的椭圆的标准方程为( )
的椭圆的标准方程为( )
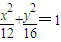
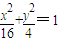
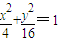
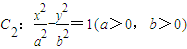 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.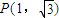 ,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t.
,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t. 是否为定值?请说明理由.
是否为定值?请说明理由. 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.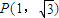 ,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t.
,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t. 是否为定值?请说明理由.
是否为定值?请说明理由. 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.