
已知A,B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A,B关于x轴对称;②A,B关于y轴对称;③A,B关于原点对称;④A,B之间的距离为4,其中正确的有( )
|
科目:初中数学 来源:2012届浙江省衢州华茂外国语学校九年级上学期期末检测数学试卷(带解析) 题型:解答题
如图,已知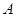 ,
,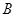 两点的坐标分别为(
两点的坐标分别为(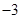 ,
, ),(
),( ,
,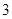 ),⊙
),⊙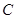 的圆心坐标为(
的圆心坐标为(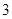 ,
, ),并与
),并与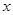 轴交于坐标原点
轴交于坐标原点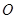 .若
.若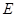 是⊙
是⊙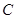 上的一个动点,线段
上的一个动点,线段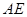 与
与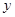 轴交于点
轴交于点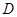 .
.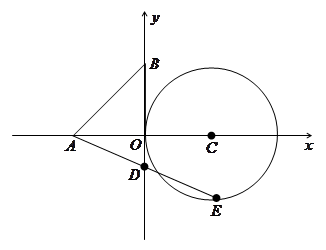
(1)线段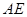 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________;
(2)当点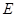 运动到点
运动到点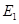 和点
和点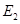 时,线段
时,线段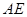 所在的直线与⊙
所在的直线与⊙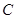 相切,求由
相切,求由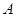
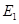 、
、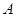
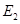 、弧
、弧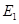
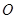
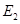 所围成的图形的面积;
所围成的图形的面积;
(3)求出△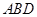 的最大值和最小值
的最大值和最小值
科目:初中数学 来源:2011-2012学年浙江省九年级上学期期末检测数学试卷(解析版) 题型:解答题
如图,已知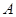 ,
,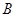 两点的坐标分别为(
两点的坐标分别为(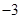 ,
, ),(
),( ,
,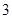 ),⊙
),⊙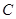 的圆心坐标为(
的圆心坐标为(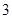 ,
, ),并与
),并与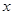 轴交于坐标原点
轴交于坐标原点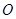 .若
.若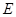 是⊙
是⊙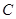 上的一个动点,线段
上的一个动点,线段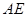 与
与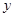 轴交于点
轴交于点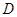 .
.
(1)线段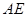 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________;
(2)当点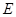 运动到点
运动到点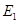 和点
和点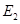 时,线段
时,线段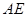 所在的直线与⊙
所在的直线与⊙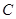 相切,求由
相切,求由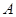
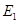 、
、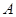
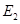 、弧
、弧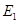
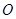
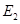 所围成的图形的面积;
所围成的图形的面积;
(3)求出△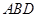 的最大值和最小值
的最大值和最小值
科目:初中数学 来源:不详 题型:解答题
 ,
, 两点的坐标分别为(
两点的坐标分别为( ,
, ),(
),( ,
, ),⊙
),⊙ 的圆心坐标为(
的圆心坐标为( ,
, ),并与
),并与 轴交于坐标原点
轴交于坐标原点 .若
.若 是⊙
是⊙ 上的一个动点,线段
上的一个动点,线段 与
与 轴交于点
轴交于点 .
.
 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________; 运动到点
运动到点 和点
和点 时,线段
时,线段 所在的直线与⊙
所在的直线与⊙ 相切,求由
相切,求由
 、
、
 、弧
、弧

 所围成的图形的面积;
所围成的图形的面积; 的最大值和最小值
的最大值和最小值科目:初中数学 来源: 题型:填空题
 已知,A、B、C、D、E是反比例函数
已知,A、B、C、D、E是反比例函数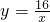 (x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是________(用含π的代数式表示).
(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是________(用含π的代数式表示).科目:初中数学 来源:浙江省月考题 题型:填空题
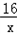 (x>0)图象上五个整数点(横,纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是( )(用含π的代数式表示).
(x>0)图象上五个整数点(横,纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是( )(用含π的代数式表示).
科目:初中数学 来源: 题型:
| k | x |
科目:初中数学 来源: 题型:
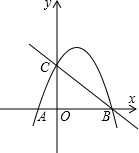 线与x轴的另一个交点.
线与x轴的另一个交点.| 1 | 2 |
科目:初中数学 来源: 题型:
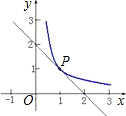 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y=| 1 |
| x |
| k |
| x |
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
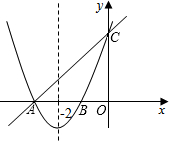 的对称轴为直线x=-2.
的对称轴为直线x=-2.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com