练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    a、b是不等于1的正数，θ∈（
    3π
    2
    ，2π），若atanθ＞btanθ＞1，则下列不等式成立的是（　　）
    A．a＞b＞1B．a＜b＜1C．b＜a＜1D．b＞a＞1
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    a、b是不等于1的正数，θ∈（
    3π
    2
    ，2π），若atanθ＞btanθ＞1，则下列不等式成立的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    a、b是不等于1的正数，θ∈（
    3π
    2
    ，2π），若atanθ＞btanθ＞1，则下列不等式成立的是（　　）
    A．a＞b＞1B．a＜b＜1C．b＜a＜1D．b＞a＞1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    a、b是不等于1的正数，θ∈（
    3π
    2
    ，2π），若atanθ＞btanθ＞1，则下列不等式成立的是（　　）
    A．a＞b＞1B．a＜b＜1C．b＜a＜1D．b＞a＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=a•bx的图象过点A（4、
    14
    ）和B（5，1）．
    （1）求函数f（x）的解析式；
    （2）记an=log2f（n）、n是正整数，Sn是数列{an}的前n项和，解关于n的不等式anSn≤0；
    （3）对于（2）中的an与Sn，整数104是否为数列{anSn}中的项？若是，则求出相应的项数；若不是，则说明理由．

    查看答案和解析>>

    科目：高中数学 来源：上海 题型：解答题

    已知函数f（x）=a•bx的图象过点A（4、
    1
    4
    ）和B（5，1）．
    （1）求函数f（x）的解析式；
    （2）记an=log2f（n）、n是正整数，Sn是数列{an}的前n项和，解关于n的不等式anSn≤0；
    （3）对于（2）中的an与Sn，整数104是否为数列{anSn}中的项？若是，则求出相应的项数；若不是，则说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

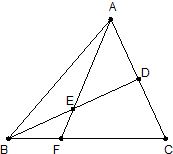    精英家教网请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．
    （1）选修4-1：几何证明选讲
    如图，在△ABC中，D是AC的中点，E是BD的中点，AE的延长线交BC于F．
    （Ⅰ）求
    BF
    FC
    的值；
    （Ⅱ）若△BEF的面积为S1，四边形CDEF的面积为S2，求S1：S2的值．
    （2）选修4-4：坐标系与参数方程
    以直角坐标系的原点O为极点，a=
    π
    6
    轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线l经过点P（1，1），倾斜角a=
    π
    6
    ．
    （ I）写出直线l的参数方程；
    （ II）设l与圆ρ=2相交于两点A、B，求点P到A、B两点的距离之积．
    （3）选修4-5：不等式选讲
    已知函数f（x）=|2x+1|+|2x-3|．
    （I）求不等式f（x）≤6的解集；
    （II）若关于x的不等式f（x）＞a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省莆田八中高三（上）第二次月考数学试卷（理科）（解析版） 题型：解答题

    本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．
    （1）选修4-2：矩阵与变换
    已知矩阵A=．
    ①求矩阵A的逆矩阵B；
    ②若直线l经过矩阵B变换后的方程为y=x，求直线l的方程．
    （2）选修4-4：坐标系与参数方程
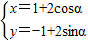    已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合．圆C的参数方程为（a为参数），点Q极坐标为（2，π）．
    （Ⅰ）化圆C的参数方程为极坐标方程；
    （Ⅱ）若点P是圆C上的任意一点，求P、Q两点距离的最小值．
    （3）选修4-5：不等式选讲
    （I）关于x的不等式|x-3|+|x-4|＜a的解不是空集，求a的取值范围．
    （II）设x，y，z∈R，且，求x+y+z的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

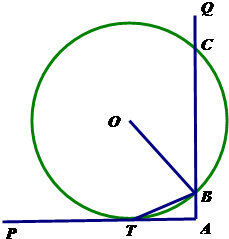    本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，
    若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
    （1）、选修4-1：几何证明选讲
    如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．求证：BT平分∠OBA
    （2）选修4-2：矩阵与变换（本小题满分10分）
    若点A（2，2）在矩阵M=
    cosα-sinα
    sinαcosα
    对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵
    （3）选修4-2：矩阵与变换（本小题满分10分）
    在极坐标系中，A为曲线ρ2+2ρcosθ-3=0上的动点，B为直线ρcosθ+ρsinθ-7=0上的动点，求AB的最小值．
    （4）选修4-5：不等式选讲（本小题满分10分）
    已知a1，a2…an都是正数，且a1•a2…an=1，求证：（2+a1）（2+a2）…（2+an）≥3n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    以下四个命题：
    ①PA、PB是平面α的两条长度相等的斜线段，则它们在平面α内的射影的长度必相等；
    ②平面α内的两直线l1、l2，若l1、l2均与平面β平行，则α∥β；
    ③若平面α内有无数个点到平面β的距离相等，则α∥β；
    ④α、β为两相交平面，且α不垂直于β，α内有一定直线l，则在平面β内有无数条直线与l垂直．
    其中正确的命题的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    以下四个命题：
    ①PA、PB是平面α的两条长度相等的斜线段，则它们在平面α内的射影的长度必相等；
    ②平面α内的两直线l1、l2，若l1、l2均与平面β平行，则α∥β；
    ③若平面α内有无数个点到平面β的距离相等，则α∥β；
    ④α、β为两相交平面，且α不垂直于β，α内有一定直线l，则在平面β内有无数条直线与l垂直．
    其中正确的命题的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>


    同步练习册答案