
 .
. (a为参数),点Q极坐标为(2,
(a为参数),点Q极坐标为(2, π).
π). ,求x+y+z的取值范围.
,求x+y+z的取值范围. ,由
,由
 =
= =
= ,求出B.
,求出B. =
=
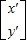 =
= ,且x′-y′=0.化简(-2x+y)-(
,且x′-y′=0.化简(-2x+y)-( -
- )=0,可得直线l的方程.
)=0,可得直线l的方程. ,-
,- ),由于圆心C的坐标为(1-1),求得CQ=
),由于圆心C的坐标为(1-1),求得CQ=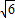 ,可得PQ的最小值为CQ-r,运算求得结果.
,可得PQ的最小值为CQ-r,运算求得结果. ,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围.
,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围. ],设矩阵A的逆矩阵B=
],设矩阵A的逆矩阵B=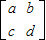 ,
,
 =
= =
= .
. ,解得
,解得  ,故A的逆矩阵B=
,故A的逆矩阵B= .
. =
=
 =
= ,且x′-y′=0.
,且x′-y′=0. -
- )=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0.
)=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0. ,化为直角坐标方程为 (x-1)2+(y+1)2=4.
,化为直角坐标方程为 (x-1)2+(y+1)2=4. π),故点Q的直角坐标为(
π),故点Q的直角坐标为( ,-
,- ).
). =
= ,点P是圆C上的任意一点,
,点P是圆C上的任意一点, -1.
-1. ,利用柯西不等式得
,利用柯西不等式得  )≥(x+y+z)2,
)≥(x+y+z)2,

科目:高中数学 来源: 题型:
|
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
| 12 |
| 3cos2θ+4sin2θ |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| 7 |
| 4 |
| x2 |
| 16 |
| y2 |
| 5 |
| z2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
a2+
|
| 2 |
| 1 |
| a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com