练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（　　）
    A．8个B．10个C．12个D．14个
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    10、设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：衢州模拟 题型：单选题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（　　）
    A．8个B．10个C．12个D．14个

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西省抚州市广昌一中、崇仁一中高一（上）期中数学试卷（解析版） 题型：选择题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（ ）
    A．8个
    B．10个
    C．12个
    D．14个

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年浙江省杭州市学军中学高一（上）期末数学试卷（解析版） 题型：选择题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（ ）
    A．8个
    B．10个
    C．12个
    D．14个

    查看答案和解析>>

    科目：高中数学 来源：2010年高考数学模拟组合试卷（3）（解析版） 题型：选择题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（ ）
    A．8个
    B．10个
    C．12个
    D．14个

    查看答案和解析>>

    科目：高中数学 来源：2010年浙江省衢州市高三4月质量检测数学试卷（理科）（解析版） 题型：选择题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为（ ）
    A．8个
    B．10个
    C．12个
    D．14个

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设A=（1，2，3，…，10），若方程x2-bx-c=0，满足b、c属于A，且方程至少有一根a属于A，称方程为漂亮方程，则“漂亮方程”的总个数为


    1. A.
      8个
    2. B.
      10个
    3. C.
      12个
    4. D.
      14个

    查看答案和解析>>

    科目：高中数学 来源：2013届山西省晋商四校高二下学期联考理科数学试卷（解析版） 题型：解答题

    设函数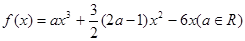

    （1）当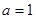时，求曲线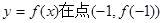处的切线方程；

    （2）当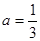时，求的极大值和极小值；

    （3）若函数在区间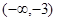上是增函数，求实数的取值范围.

    【解析】（1）中，先利用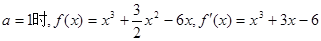，表示出点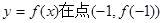的斜率值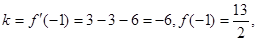这样可以得到切线方程。（2）中，当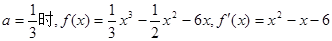，再令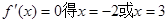，利用导数的正负确定单调性，进而得到极值。（3）中，利用函数在给定区间递增，说明了在区间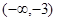导数恒大于等于零，分离参数求解范围的思想。

    解：（1）当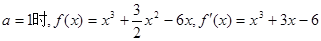……2分

        ∴

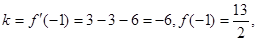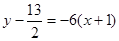
    即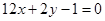为所求切线方程。………………4分

    （2）当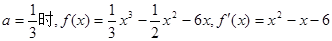

    令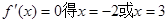………………6分

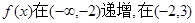    ∴递减，在（3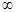，+）递增

    ∴的极大值为…………8分

    （3）

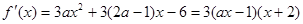
    ①若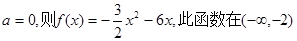上单调递增。∴满足要求。…10分

    ②若

    ∵恒成立，

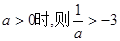    恒成立，即a>0……………11分

    时，不合题意。综上所述，实数的取值范围是

     

    查看答案和解析>>

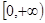
    科目：高中数学 来源： 题型：

    已知圆Mx2+y2-2tx-6t-10=0，椭圆C：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0），若椭圆C与x轴的交点A（5，y0）到其右准线的距离为
    10
    3
    ；点A在圆M外，且圆M上的点和点A的最大距离与最小距离之差为2．
    （1）求圆M的方程和椭圆C的方程；
    （2）设点P为椭圆C上任意一点，自点P向圆M引切线，切点分别为A、B，请试着去求
    P
    A•
    P
    B    的取值范围；
    （3）设直线系M：xcosθ+（y-3）sinθ=1（θ∈R）；求证：直线系M中的任意一条直线l恒与定圆相切，并直接写出三边都在直线系M中的直线上的所有可能的等腰直角三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省南通市海门中学高三（上）开学检测数学试卷（解析版） 题型：解答题

    【选做题】在A，B，C，D四小题中只能选做2题，每题10分，共计20分．请在答题卡指定区域内作答，解答时写出文字说明、证明过程或演算步骤．
    21-1．（选修4-2：矩阵与变换）
    设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
    （1）求矩阵M的特征值及相应的特征向量；
    （2）求逆矩阵M-1以及椭圆+=1在M-1的作用下的新曲线的方程．
    21-2．（选修4-4：参数方程）
    以直角坐标系的原点O为极点，x轴的正半轴为极轴．已知点P的直角坐标为（1，-5），点M的极坐标为（4，），若直线l过点P，且倾斜角为 ，圆C以M为圆心、4为半径．
    （1）求直线l关于t的参数方程和圆C的极坐标方程；
    （2）试判定直线l和圆C的位置关系．

    查看答案和解析>>


    同步练习册答案