
| 下列说法中,正确的个数为( ) ①函数y=f(x)与函数y=f(-x)的图象关于直线x=0对称; ②函数y=f(x)与函数y=-f(x)的图象关于直线y=0对称; ③函数y=f(x)与函数y=-f(-x)的图象关于坐标原点对称; ④如果函数y=f(x)对于一切x∈R,都有f(a+x)=f(a-x),那么y=f(x)的图象关于直线x=a对称.
|
科目:高中数学 来源:2013年高考数学复习卷E(二)(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| 1 | 2 |
科目:高中数学 来源:不详 题型:填空题
| 1 |
| 2 |
科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:选择题
 ,则x=g(t)是f(x)的一个等值域变换;
,则x=g(t)是f(x)的一个等值域变换;科目:高中数学 来源:2012-2013学年山东省临沂市映达高考补习学校高三一轮复习期中迎考数学模拟试卷1(理科)(解析版) 题型:填空题
 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心; ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:选择题
 ,则x=g(t)是f(x)的一个等值域变换;
,则x=g(t)是f(x)的一个等值域变换;科目:高中数学 来源:2012-2013学年山东省临沂市映达高考补习学校高三一轮复习期中迎考数学模拟试卷1(理科)(解析版) 题型:填空题
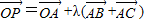 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;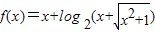 ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.科目:高中数学 来源: 题型:单选题
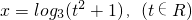 ,则x=g(t)是f(x)的一个等值域变换;
,则x=g(t)是f(x)的一个等值域变换;科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x |
| 1+|x| |
| 5 |
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 8 |
| π |
| 4 |
| π |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com