| 在三棱锥S-ABC中,侧棱SC⊥平面SAB,SA⊥BC,侧面△SAB,△SBC,△SAC的面积分别为1,,3,则此三棱锥的外接球的表面积为( ) |
相关习题
科目:高中数学
来源:
题型:
在三棱锥S-ABC中,侧棱SC⊥平面SAB,SA⊥BC,侧面△SAB,△SBC,△SAC的面积分别为1,
,3,则此三棱锥的外接球的表面积为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在三棱锥S-ABC中,侧棱SC⊥平面SAB,SA⊥BC,侧面△SAB,△SBC,△SAC的面积分别为1,
,3,则此三棱锥的外接球的表面积为( )
查看答案和解析>>
科目:高中数学
来源:2013年高考数学备考复习卷8:立体几何(解析版)
题型:选择题
在三棱锥S-ABC中,侧棱SC⊥平面SAB,SA⊥BC,侧面△SAB,△SBC,△SAC的面积分别为1,

,3,则此三棱锥的外接球的表面积为( )
A.14π
B.
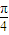
C.
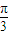
D.
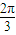
查看答案和解析>>
科目:高中数学
来源:
题型:
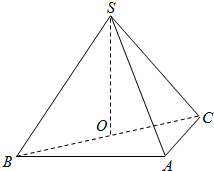
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A-SC-B的余弦值.
查看答案和解析>>
科目:高中数学
来源:
题型:
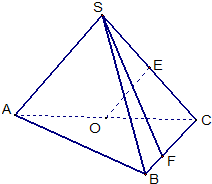
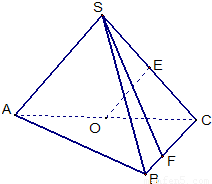
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=
,BC=
AC,∠ASC=∠ACB=90°.
(1)求证:OE∥平面SAB;
(2)若点F在线段BC上,问:无论F在BC的何处,是否都有OE⊥SF?请证明你的结论;
(3)求二面角B-AS-C的平面角的余弦值.
查看答案和解析>>
科目:高中数学
来源:期末题
题型:解答题
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90 °,O为BC的中点.
(1) 证明:SO⊥平面ABC ;
(2) 求二面角A-SC-B的余弦值
查看答案和解析>>
科目:高中数学
来源:0127 模拟题
题型:解答题
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点。
(1)证明:SO⊥平面ABC;
(2)求二面角A-SC-B的余弦值。
查看答案和解析>>
科目:高中数学
来源:2007-2008学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)(解析版)
题型:解答题

如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A-SC-B的余弦值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市海淀区八一中学高三(上)周练数学试卷(11)(理科)(解析版)
题型:解答题
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=
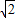
,BC=

AC,∠ASC=∠ACB=90°.
(1)求证:OE∥平面SAB;
(2)若点F在线段BC上,问:无论F在BC的何处,是否都有OE⊥SF?请证明你的结论;
(3)求二面角B-AS-C的平面角的余弦值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市东城区示范校高三(上)12月联考数学试卷(理科)(解析版)
题型:解答题
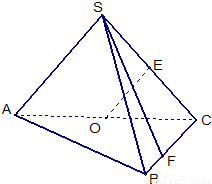
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=
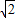
,BC=

AC,∠ASC=∠ACB=90°.
(1)求证:OE∥平面SAB;
(2)若点F在线段BC上,问:无论F在BC的何处,是否都有OE⊥SF?请证明你的结论;
(3)求二面角B-AS-C的平面角的余弦值.
查看答案和解析>>

 ,3,则此三棱锥的外接球的表面积为( )
,3,则此三棱锥的外接球的表面积为( )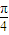
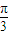
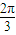
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=

 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.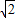 ,BC=
,BC= AC,∠ASC=∠ACB=90°.
AC,∠ASC=∠ACB=90°.
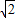 ,BC=
,BC= AC,∠ASC=∠ACB=90°.
AC,∠ASC=∠ACB=90°.