
科目:初中数学 来源:轻松练习30分(测试卷) 初三代数下册 题型:013
老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质
甲:这个函数的图象关于直线x=1对称;
乙:当x<0时,y的值随x的增大而减小;
丙:当x>0时,y的值随x的增大而增大;
丁:当x=0时,y的值不是函数的最小值.
如果其中恰有三人说得正确,那么这个函数可能是
[ ]
科目:初中数学 来源: 题型:013
老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质
甲:这个函数的图象关于直线x=1对称;
乙:当x<0时,y的值随x的增大而减小;
丙:当x>0时,y的值随x的增大而增大;
丁:当x=0时,y的值不是函数的最小值.
如果其中恰有三人说得正确,那么这个函数可能是
[ ]
科目:初中数学 来源:2008年山东省青岛市初中毕业升学统一考试、数学试卷 题型:044
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
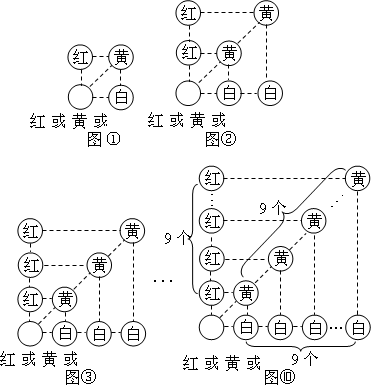
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:1+3=4(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是:1+3×2=7(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是:1+3×3=10(如图③):
……
(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:1+3×(10-1)=28(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是________;
(3)若要确保摸出的小球至少有n个同色(n<20),则最少需摸出小球的个数是________.
模型拓展二:在不透明口袋中装有m种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________.
(2)若要确保摸出的小球至少有n个同色(n<20),则最少需摸出小球的个数是________.
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
科目:初中数学 来源:2013年江苏省苏州市吴江市中考数学模拟试卷(5月份)(解析版) 题型:解答题

科目:初中数学 来源: 题型:
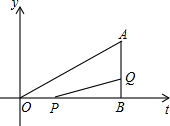 (2013•吴江市模拟)如图所示,点B坐标为(18,0),点A坐标为(18,6),动点P从点O开始沿OB以每秒3个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒1个单位长度的速度向点A移动.如果P、Q分别从O、B同时出发,用t(秒)表示移动的时间(0<t≤6),那么,
(2013•吴江市模拟)如图所示,点B坐标为(18,0),点A坐标为(18,6),动点P从点O开始沿OB以每秒3个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒1个单位长度的速度向点A移动.如果P、Q分别从O、B同时出发,用t(秒)表示移动的时间(0<t≤6),那么,科目:初中数学 来源: 题型:
 (0<t≤6),那么,
(0<t≤6),那么,科目:初中数学 来源: 题型:解答题
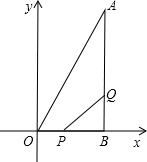 (0<t≤6),那么,
(0<t≤6),那么,湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com