
若实数a∈(1,2),则使得函数f(x)=
|
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、(1,+∞) |
| B、(0,a-1) |
| C、(0,1) |
| D、(a-1,1) |
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| A.(1,+∞) | B.(0,a-1) | C.(0,1) | D.(a-1,1) |
科目:高中数学 来源:2012年福建省莆田市高中毕业班教学质量检查数学试卷(理科)(解析版) 题型:选择题


科目:高中数学 来源:2011-2012学年湖南省十二校高三(下)4月联考数学试卷(理科)(解析版) 题型:选择题
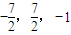

科目:高中数学 来源:佛山二模 题型:解答题
| x |
| y |
| y |
| x |
| n |
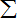 |
| k-2 |
| 1 |
| k |
| n-1 |
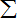 |
| k-1 |
| 1 |
| k |
| x+y |
| 2 |
科目:高中数学 来源:2012-2013学年山东省济宁市鱼台一中高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,函数
,函数 ,若存在
,若存在 ,使得f(x1)=g(x2)成立,则实数m的取值范围是( )
,使得f(x1)=g(x2)成立,则实数m的取值范围是( )

科目:高中数学 来源:2012-2013学年福建省莆田市仙游一中高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 .
. (t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为 .
. (其中O为坐标原点)?若存在,请求出;否则,请说明理由.
(其中O为坐标原点)?若存在,请求出;否则,请说明理由.科目:高中数学 来源:2012-2013学年四川省遂宁市射洪中学高三(上)第三次月考数学试卷(文科)(解析版) 题型:选择题
 ,函数
,函数 ,若存在
,若存在 ,使得f(x1)=g(x2)成立,则实数m的取值范围是( )
,使得f(x1)=g(x2)成立,则实数m的取值范围是( )

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com