下列说法:
①若一元二次方程x2+bx+a=0有一个根是-a(a≠0),则代数式a-b的值是-1
②若a+b+c=0,则x=a+b+c是一元二次方程ax2+bx+c=0的一个根
③若b=2a+3c,则一元二次方程ax2+bx+c=0有不相等的两个实数根
④当m取整数-1或1时,关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的解都是整数.
其中正确的有( ) |
相关习题
科目:初中数学
来源:2009-2010学年贵州省安顺市幺铺中学九年级(上)第一次月考数学试卷(解析版)
题型:选择题
下列说法:
①
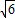
是二次根式,但不是整式;
②方程x
2-x-k=0的根为
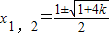
;
③若ac<0,则方程ax
2+bx+c=0方程必有实数根;
④课本第54页观察与猜想讨论了一元二次方程根与系数的关系,根据这一关系得方程x
2-3x+5=0的两根和是3,两根积是5.
其中错误的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学
来源:
题型:
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2
,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
0是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
0+b)
2,其中正确的( )
| A、只有①②③ | B、只有①②④ |
| C、①②③④ | D、只有③④ |
查看答案和解析>>
科目:初中数学
来源:
题型:
对于一元二次方程ax2+bx+c=0,下列说法正确的有( )
①若a:b:c=1:2:1,则方程必有两个相等的实根;②若x1=2,x2=-1是方程的两根,则b=-a,c=-2a;
③若b=3a,c=2a,则方程两个根必为x1=-1,x2=-2;④若方程一个实根为x=c,则必有ac=-b-1.
查看答案和解析>>
科目:初中数学
来源:不详
题型:单选题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2
,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
0是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
0+b)
2,其中正确的( )
| A.只有①②③ | B.只有①②④ | C.①②③④ | D.只有③④ |
查看答案和解析>>
科目:初中数学
来源:第2章《一元二次方程》好题集(07):2.3 公式法(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2
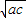
,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>
科目:初中数学
来源:第28章《一元二次方程》好题集(06):28.2 解一元二次方程(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2

,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>
科目:初中数学
来源:第1章《一元二次方程》好题集(06):1.2 解一元二次方程的算法(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2

,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>
科目:初中数学
来源:第4章《一元二次方程》好题集(06):4.2 一元二次方程的解法(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2

,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>
科目:初中数学
来源:第23章《一元二次方程》好题集(06):23.2 一元二次方程的解法(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2

,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>
科目:初中数学
来源:第22章《一元二次方程》好题集(06):22.2 降次——解一元二次方程(解析版)
题型:选择题
对于一元二次方程ax
2+bx+c=0(a≠0),下列说法:
①若b=2

,则方程ax
2+bx+c=0一定有两个相等的实数根;
②若方程ax
2+bx+c=0有两个不等的实数根,则方程x
2-bx+ac=0也一定有两个不等的实数根;
③若c是方程ax
2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x
是一元二次方程ax
2+bx+c=0的根,则b
2-4ac=(2ax
+b)
2,其中正确的( )
A.只有①②③
B.只有①②④
C.①②③④
D.只有③④
查看答案和解析>>

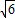 是二次根式,但不是整式;
是二次根式,但不是整式;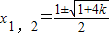 ;
;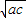 ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根; ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根; ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根; ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根; ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根; ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根;