命题P:“?a∈R,则a2≤0”,则¬P为( )| A.?a∈R,a2>0 | B.?a∈R,a2≤0 | C.?a∈R,a2>0 | D.?a∈R,a2≤0. |
|
相关习题
科目:高中数学
来源:
题型:
命题P:“?a∈R,则a2≤0”,则¬P为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
命题P:“?a∈R,则a
2≤0”,则¬P为( )
| A.?a∈R,a2>0 | B.?a∈R,a2≤0 | C.?a∈R,a2>0 | D.?a∈R,a2≤0. |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省合肥市长丰县高二(上)期末数学试卷(文科)(解析版)
题型:选择题
命题P:“?a∈R,则a2≤0”,则¬P为( )
A.?a∈R,a2>0
B.?a∈R,a2≤0
C.?a∈R,a2>0
D.?a∈R,a2≤0.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年山东省淄博一中高三(上)期末数学试卷(理科)(解析版)
题型:选择题
下列命题中的真命题的个数是( )
(1)命题“若x=1,则x
2+x-2=0”的否命题为“若x=1,则x
2+x-2≠0”;
(2)若命题p:?x
∈(-∞,0],

≥1,则¬p:?x∈(0,+∞),(

)
x<1;
(3)设命题p:?x
∈(0,∞),log
2x
<log
3x
,命题q:?x∈(0,

),tanx>sinx则p∧q为真命题;
(4)设a,b∈R,那么“ab+1>a+b”是“a
2+b
2<1”的必要不充分条件.
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:高中数学
来源:
题型:
给出下列结论:
①命题“若a
2+b
2=0(a,b∈R),则a=b=0”的逆否命题为“若a≠0且b≠0.(a,b∈R),则a
2+b
2≠0.”
②给定p:
>0则¬p为
≤0③命题“正方形的四个内角相等”的否命题为假.
④“x
2-3x+2≠0”是“x≠1的必要不充分条件”.
其中正确的结论是
③
③
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
给出下列结论:
①命题“若a
2+b
2=0(a,b∈R),则a=b=0”的逆否命题为“若a≠0且b≠0.(a,b∈R),则a
2+b
2≠0.”
②给定p:
>0则¬p为
≤0③命题“正方形的四个内角相等”的否命题为假.
④“x
2-3x+2≠0”是“x≠1的必要不充分条件”.
其中正确的结论是______.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省南京市新城中学高三(上)第一次月考数学试卷(理科)(解析版)
题型:填空题
给出下列结论:
①命题“若a
2+b
2=0(a,b∈R),则a=b=0”的逆否命题为“若a≠0且b≠0.(a,b∈R),则a
2+b
2≠0.”
②给定p:
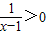
则¬p为
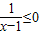
③命题“正方形的四个内角相等”的否命题为假.
④“x
2-3x+2≠0”是“x≠1的必要不充分条件”.
其中正确的结论是
.
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
给出下列结论:
①命题“若a2+b2=0(a,b∈R),则a=b=0”的逆否命题为“若a≠0且b≠0.(a,b∈R),则a2+b2≠0.”
②给定p: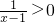 则¬p为
则¬p为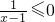
③命题“正方形的四个内角相等”的否命题为假.
④“x2-3x+2≠0”是“x≠1的必要不充分条件”.
其中正确的结论是________.
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
下列命题中的真命题的个数是
(1)命题“若x=1,则x2+x-2=0”的否命题为“若x=1,则x2+x-2≠0”;
(2)若命题p:?x0∈(-∞,0],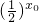 ≥1,则¬p:?x∈(0,+∞),(
≥1,则¬p:?x∈(0,+∞),( )x<1;
)x<1;
(3)设命题p:?x0∈(0,∞),log2x0<log3x0,命题q:?x∈(0,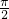 ),tanx>sinx则p∧q为真命题;
),tanx>sinx则p∧q为真命题;
(4)设a,b∈R,那么“ab+1>a+b”是“a2+b2<1”的必要不充分条件.
- A.
3个
- B.
2个
- C.
1个
- D.
0个
查看答案和解析>>
科目:高中数学
来源:
题型:
下列命题中的真命题的个数是( )
(1)命题“若x=1,则x
2+x-2=0”的否命题为“若x=1,则x
2+x-2≠0”;
(2)若命题p:?x
0∈(-∞,0],
()x0≥1,则¬p:?x∈(0,+∞),(
)
x<1;
(3)设命题p:?x
0∈(0,∞),log
2x
0<log
3x
0,命题q:?x∈(0,
),tanx>sinx则p∧q为真命题;
(4)设a,b∈R,那么“ab+1>a+b”是“a
2+b
2<1”的必要不充分条件.
查看答案和解析>>

 ≥1,则¬p:?x∈(0,+∞),(
≥1,则¬p:?x∈(0,+∞),( )x<1;
)x<1; ),tanx>sinx则p∧q为真命题;
),tanx>sinx则p∧q为真命题;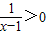 则¬p为
则¬p为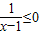
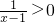 则¬p为
则¬p为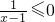
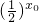 ≥1,则¬p:?x∈(0,+∞),(
≥1,则¬p:?x∈(0,+∞),( )x<1;
)x<1;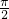 ),tanx>sinx则p∧q为真命题;
),tanx>sinx则p∧q为真命题;