| 已知定义在R上的函数f(x)是奇函数,且满足f(x+2)+2f(-x)=0;给出下列结论:①f(2)=0②f(x+2)=2f(x)③f(x+4)=4f(x)④f(x+6)=6f(x)其中正确的结论的个数是( ) |
相关习题
科目:高中数学
来源:
题型:
已知定义在R上的函数f(x)是奇函数,且f(x+2)=f(x)-f(2),则f(-8)=( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知定义在R上的函数f(x)是奇函数,且满足f(x+2)+2f(-x)=0;给出下列结论:①f(2)=0②f(x+2)=2f(x)③f(x+4)=4f(x)④f(x+6)=6f(x)其中正确的结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知定义在R上的函数f(x)是奇函数,且当x≤0时,f(x)=2x+x+a,则f(2)的值为( )
查看答案和解析>>
科目:高中数学
来源:河东区一模
题型:单选题
已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有
<0,则不等式x
2•f(x)>0的解集是( )
| A.(-2,0)∪(2,+∞) | B.(-∞,-2)∪(0,2) | C.(-2,0)∪(0,2) | D.(-2,2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知定义在R上的函数f(x)是奇函数,且满足f(x+2)+2f(-x)=0;给出下列结论:①f(2)=0②f(x+2)=2f(x)③f(x+4)=4f(x)④f(x+6)=6f(x)其中正确的结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省东莞中学高二(下)期末数学试卷(文科)(解析版)
题型:选择题
已知定义在R上的函数f(x)是奇函数,且满足f(x+2)+2f(-x)=0;给出下列结论:①f(2)=0②f(x+2)=2f(x)③f(x+4)=4f(x)④f(x+6)=6f(x)其中正确的结论的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:2010年天津市河东区高考数学一模试卷(文科)(解析版)
题型:选择题
已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有

,则不等式x
2•f(x)>0的解集是( )
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(0,2)
C.(-2,0)∪(0,2)
D.(-2,2)∪(2,+∞)
查看答案和解析>>
科目:高中数学
来源:2009年山东省潍坊市高考数学二模试卷(理科)(解析版)
题型:选择题
已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有

,则不等式x
2•f(x)>0的解集是( )
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(0,2)
C.(-2,0)∪(0,2)
D.(-2,2)∪(2,+∞)
查看答案和解析>>
科目:高中数学
来源:2009年山东省潍坊市高考数学二模试卷(文科)(解析版)
题型:选择题
已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有

,则不等式x
2•f(x)>0的解集是( )
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(0,2)
C.(-2,0)∪(0,2)
D.(-2,2)∪(2,+∞)
查看答案和解析>>
科目:高中数学
来源:2010年山东省高考数学压轴卷1(理科)(解析版)
题型:选择题
已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有
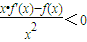
,则不等式x
2•f(x)>0的解集是( )
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(0,2)
C.(-2,0)∪(0,2)
D.(-2,2)∪(2,+∞)
查看答案和解析>>

 ,则不等式x2•f(x)>0的解集是( )
,则不等式x2•f(x)>0的解集是( ) ,则不等式x2•f(x)>0的解集是( )
,则不等式x2•f(x)>0的解集是( ) ,则不等式x2•f(x)>0的解集是( )
,则不等式x2•f(x)>0的解集是( )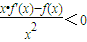 ,则不等式x2•f(x)>0的解集是( )
,则不等式x2•f(x)>0的解集是( )