
如果直线上一点到⊙O的圆心O的距离大于⊙O的半径,那么这条直线与⊙O的位置关系是( )
|
科目:初中数学 来源:静安区二模 题型:单选题
| A.相交 |
| B.相切 |
| C.相离 |
| D.相交、相切、相离都有可能 |
科目:初中数学 来源:2010年上海市静安区时代中学中考数学模拟试卷(解析版) 题型:选择题
科目:初中数学 来源:2008年上海市静安区中考数学二模试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:
| 10 |
| 9 |
| 10 |
| 9 |
科目:初中数学 来源: 题型:
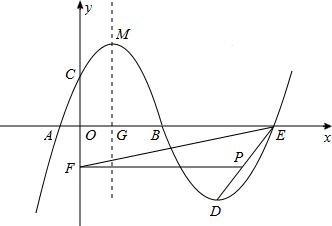
如图8,抛物线![]() :
:![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,将抛物线
,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() ,它的顶点为
,它的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)设抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(
上一个动点(![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .如果
.如果![]() 点的坐标为
点的坐标为![]() ,
,![]() 的面积为S,求S与
的面积为S,求S与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围,并求出S的最大值;
的取值范围,并求出S的最大值;
(3)设抛物![]() 线
线![]() 的对称轴与
的对称轴与![]() 轴的交点为
轴的交点为![]() ,以
,以![]() 为圆心,
为圆心,![]() 两点间的距离为直径作⊙
两点间的距离为直径作⊙![]() ,试判断直线
,试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由.
的位置关系,并说明理由.

科目:初中数学 来源:中考真题 题型:解答题
 (x+h )2+k 与x 轴的交点为A 、B ,与y 轴的交点为C ,顶点为M (3,
(x+h )2+k 与x 轴的交点为A 、B ,与y 轴的交点为C ,顶点为M (3, ),将抛物线m 绕点B旋转180°,得到新的抛物线n,它的顶点为D。
),将抛物线m 绕点B旋转180°,得到新的抛物线n,它的顶点为D。
科目:初中数学 来源:2012年湖南省怀化市中考数学试卷(解析版) 题型:解答题
 (x+h)2+k与x轴的交点为A、B,与y轴的交点为C,顶点为M(3,
(x+h)2+k与x轴的交点为A、B,与y轴的交点为C,顶点为M(3, ),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D;
),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D;
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 25 |
| 4 |
 ⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
⊙G,试判断直线CM与⊙G的位置关系,并说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com