练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等比数列{an}中，0＜a1＜a4=1，使不等式(a1-
    1
    a1
    )+(a2-
    1
    a2
    )+…+(an-
    1
    an
    )≤0    成立的最大自然数是（　　）
    A．5B．6C．7D．8
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：资阳一模 题型：单选题

    在等比数列{an}中，0＜a1＜a4=1，使不等式(a1-
    1
    a1
    )+(a2-
    1
    a2
    )+…+(an-
    1
    an
    )≤0    成立的最大自然数是（　　）
    A．5B．6C．7D．8

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省莆田一中高三（上）期末数学试卷（文科）（解析版） 题型：选择题

    在等比数列{an}中，0＜a1＜a4=1，使不等式成立的最大自然数是（ ）
    A．5
    B．6
    C．7
    D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在等比数列{an}中，0＜a1＜a4=1，使不等式数学公式成立的最大自然数是


    1. A.
      5
    2. B.
      6
    3. C.
      7
    4. D.
      8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•资阳一模）在等比数列{an}中，0＜a1＜a4=1，使不等式(a1-
    1
    a1
    )+(a2-
    1
    a2
    )+…+(an-
    1
    an
    )≤0    成立的最大自然数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在正项等比数列an中，a1＜a4=1，若集合A={n|(a1-
    1
    a1
    )+(a2-
    1
    a2
    )+…+(an-
    1
    an
    )≤0，n∈N*}    ，则集合A中元素的个数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在正项等比数列an中，a1＜a4=1，若集合A={n|(a1-
    1
    a1
    )+(a2-
    1
    a2
    )+…+(an-
    1
    an
    )≤0，n∈N*}    ，则集合A中元素的个数为______．

    查看答案和解析>>

    科目：高中数学 来源：2012年河南省焦作市高三第一次质量检测数学试卷（理科）（解析版） 题型：解答题

    在公比为2的等比数列{an}中，a2与a4的等差中项是．
    （Ⅰ）求a1的值；
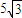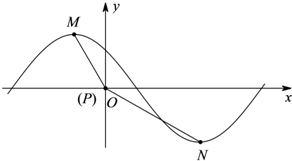
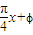    （Ⅱ）若函数y=|a1|sin（），|ϕ|＜π的一部分图象如图所示，M（-1，|a1|），为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

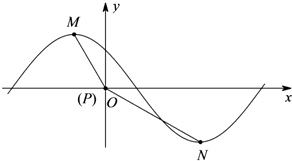    在公比为2的等比数列{an}中，a2与a4的等差中项是数学公式．
    （Ⅰ）求a1的值；
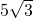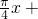    （Ⅱ）若函数y=|a1|sin（数学公式），|?|＜π的一部分图象如图所示，M（-1，|a1|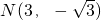），数学公式为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•焦作模拟）在公比为2的等比数列{an}中，a2与a4的等差中项是5
    		3
    ．
    （Ⅰ）求a1的值；
    （Ⅱ）若函数y=|a1|sin（
    π
    4
    x+?    ），|?|＜π的一部分图象如图所示，M（-1，|a1|），N(3，-
    		3
    )    为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在数列{an}中，a1=0，且对任意k∈N*，a2k-1，a2k，a2k+1成等差数列，其公差为2k．
    （Ⅰ）证明a4，a5，a6成等比数列；
    （Ⅱ）求数列{an}的通项公式；
    （Ⅲ）记Tn=
    22
    a2
    +
    32
    a3
    +…+
    n2
    an
    ，证明
    3
    2
    ＜2n-Tn≤2(n≥2)    ．

    查看答案和解析>>


    同步练习册答案